
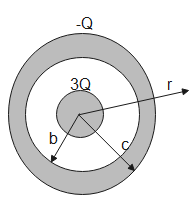
Consider a spherical Gaussian surface of radius $r > c$, the net charge enclosed by this surface is $Y\times Q$. Find the value of $Y$?

Answer
529.5k+ views
Hint: The given figure is two concentric spheres with different charges on their surface. The Gaussian surface is drawn such that the electric lines of forces are perpendicular to its surface. The charge enclosed within the Gaussian surface is the total charge on the body.
Complete answer:
A Gaussian surface is an imaginary surface drawn around an object such that the electric lines of forces are perpendicular to the Gaussian surface. The charge enclosed within a Gaussian surface accounts for the flux emerging from it. For the given figure, it is a spherical shell and hence its Gaussian surface will be a sphere.
Electric lines of forces are the curves that emerge from positive charge and end into the negative charge. They represent the electric field for that surface.
Due to 3Q, the charge induced on the outer sphere will be- +3Q on the inner surface and -3Q on the outer surface. Therefore, total induced charge is $3Q-3Q=0$.
The total charge on the sphere body is $3Q-2Q=Q$.
The charge enclosed in the Gaussian surface is the total charge which is given as-
$\begin{align}
& Y\times Q=Q \\
& \therefore Y=1 \\
\end{align}$
The value of $Y$ is 1.
Therefore, the total charge enclosed within the Gaussian surface is $Q$ and the value of $Y$ is 1.
Note:
The whole charge of a metallic body is concentrated at its surface, charge inside it is zero, therefore, the electric field inside a metallic body is zero and the potential is constant. According to Gauss’s law, the flux coming out of a surface depends on the charge enclosed inside it.
Complete answer:
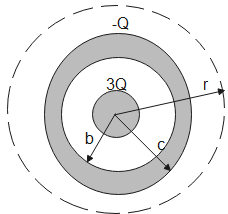
A Gaussian surface is an imaginary surface drawn around an object such that the electric lines of forces are perpendicular to the Gaussian surface. The charge enclosed within a Gaussian surface accounts for the flux emerging from it. For the given figure, it is a spherical shell and hence its Gaussian surface will be a sphere.
Electric lines of forces are the curves that emerge from positive charge and end into the negative charge. They represent the electric field for that surface.

Due to 3Q, the charge induced on the outer sphere will be- +3Q on the inner surface and -3Q on the outer surface. Therefore, total induced charge is $3Q-3Q=0$.
The total charge on the sphere body is $3Q-2Q=Q$.
The charge enclosed in the Gaussian surface is the total charge which is given as-
$\begin{align}
& Y\times Q=Q \\
& \therefore Y=1 \\
\end{align}$
The value of $Y$ is 1.
Therefore, the total charge enclosed within the Gaussian surface is $Q$ and the value of $Y$ is 1.
Note:
The whole charge of a metallic body is concentrated at its surface, charge inside it is zero, therefore, the electric field inside a metallic body is zero and the potential is constant. According to Gauss’s law, the flux coming out of a surface depends on the charge enclosed inside it.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




