Question

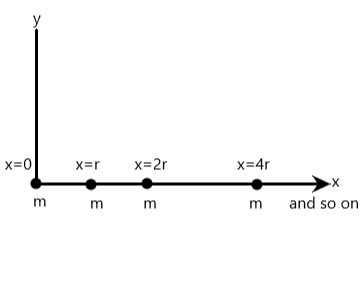
Consider an infinite distribution of point masses (each of mass \[m\]) placed on the x axis as shown in the diagram. What is the gravitational force acting on the point mass placed at the origin?

A. \[\dfrac{{4G{m^2}}}{{3{r^2}}}\]
B. \[\dfrac{{G{m^2}}}{{3{r^2}}}\]
C. \[\dfrac{{4G{m^2}}}{{{r^2}}}\]
D. \[\dfrac{{G{m^2}}}{{{r^2}}}\]

Answer 1

Hint: We need to use Newton's universal law of gravitation to find the force on the mass at the origin due to the other individual masses on the x axis. The sum of the forces is a geometric progression with a sum to infinity.

Formula used: In this solution we will be using the following formulae;
\[F = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\] where \[F\] is the gravitational force of attraction between two bodies, \[{m_1}\] and \[{m_2}\] are the masses of the two bodies, and \[r\] is the distance between them (their centres for non-point masses).
\[{S_\infty } = \dfrac{a}{{1 - r}}\] for \[0 < r < 1\] where \[{S_\infty }\] is the sum to infinity of a geometric series\[a\] is the first term of the series and \[r\] is the common ratio.

Complete step by step answer:
We see an infinite arrangement of point masses and we are to find the force due to this infinite array on the mass at the origin.
To do so, we use the Newton’s law which mathematically can be given as
\[F = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\] where \[F\] is the gravitational force of attraction between two bodies, \[{m_1}\] and \[{m_2}\] are the masses of the two bodies, and \[r\] is the distance between them.
Hence, we have for the first mass to be
\[{F_1} = \dfrac{{Gmm}}{{{r^2}}}\]
Similarly for the second mass on the origin mass we have
\[{F_2} = \dfrac{{Gmm}}{{{{\left( {2r} \right)}^2}}} = \dfrac{{Gmm}}{{4{r^2}}}\]
Also, for the third mass
\[{F_3} = \dfrac{{Gmm}}{{{{\left( {4r} \right)}^2}}} = \dfrac{{Gmm}}{{16{r^2}}}\]
But the force is the sum of all the individual forces as in
\[F = {F_1} + {F_2} + {F_3} + ...\] since it continues to infinity.
Hence, we have that
\[ \Rightarrow F = \dfrac{{Gmm}}{{{r^2}}}\left[ {\dfrac{1}{1} + \dfrac{1}{4} + \dfrac{1}{{16}} + ...} \right]\]
If observed, the sum in the bracket is a geometric progression with a common ratio of \[\dfrac{1}{4}\]
Also, the sum to infinity of a geometric progression can be given as
\[{S_\infty } = \dfrac{a}{{1 - r}}\] for \[0 < r < 1\] where \[a\] is the first term of the series and \[r\] is the common ratio. Hence inserting known values
\[{S_\infty } = \dfrac{1}{{1 - \dfrac{1}{4}}}\]
\[ \Rightarrow {S_\infty } = \dfrac{1}{{1 - \dfrac{1}{4}}} = \dfrac{1}{{\dfrac{3}{4}}} = \dfrac{4}{3}\].
Hence,
\[F = \dfrac{{Gmm}}{{{r^2}}}\left[ {\dfrac{4}{3}} \right]\]
\[ \Rightarrow F = \dfrac{{4G{m^2}}}{{3{r^2}}}\]
Hence, the correct option is A.

Note: Note that in actuality, the masses cannot be to a literal infinity. The term infinity is used in this case to denote that the masses are numerous. Also, the common ratio is gotten from dividing any of the term by the preceding term as in
\[r = \dfrac{1}{4} \div 1 = \dfrac{1}{{16}} \div \dfrac{1}{4} = \dfrac{1}{4}\]