Question

Consider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in figure. The temperature of the gas at A and B are 300 K and 500 K respectively. A total of 1200 J heat is withdrawn from the sample in the process. Find the work done by the gas in part BC. Take R=8.3 J/mol−K.

Answer 1

Hint: We can use the first law of thermodynamics to solve this question. According to the first law of thermodynamics the internal energy of a system is the sum of the total energy given to the system and the work done by the system. This is also known as the law of conservation of energy. Another important point to note is that since this is a cyclic process the change in internal energy for this system is going to be zero.

Complete answer:
 From first law of thermodynamics we can say that,
 \[\Delta U = q + W\]
We know that the change in internal energy of any system during a cyclic process is zero. Therefore we can say that the heat supplied to the gas is equal to work done by the gas.
\[ \Rightarrow q = - W\]
We are provided with the data that the heat withdrawn from the sample is -1200 J. So we can modify the equation as:
 \[ \Rightarrow {W_{Total}} = - ( - 1200) = + 1200J\]
As all the cyclic processes are traced anticlockwise, the net work done by the system will be negative.
\[ \Rightarrow W = - 1200\]
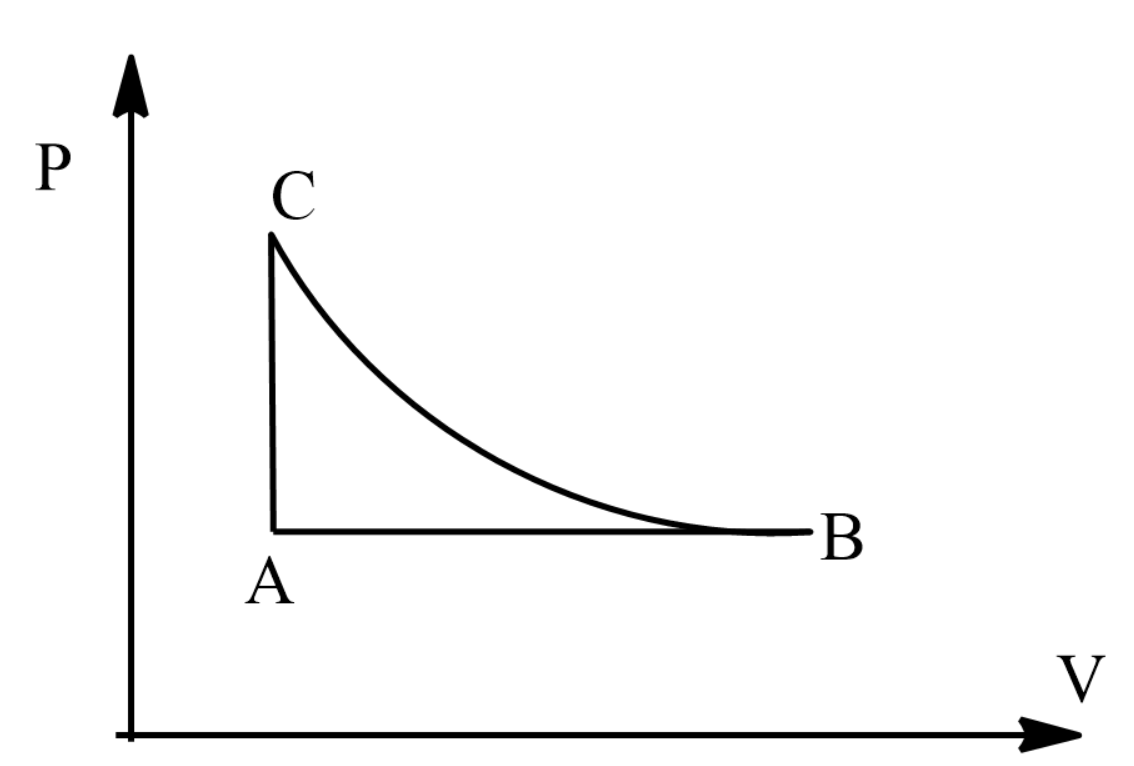
Now from the figure we can say that the total work will be the sum of all the works from A to C in a cyclic manner.
Work done during process A to B,
\[ \Rightarrow {W_{A \to B}} = P\Delta V = nR\Delta T\]
\[ \Rightarrow {W_{A \to B}} = nR({T_B} - {T_A})\]
\[ \Rightarrow {W_{A \to B}} = 2 \times 8.314 \times (500 - 300)\]
\[ \Rightarrow {W_{A \to B}} = 3325.6J\]
 Now work done during process C to A,
\[ \Rightarrow {W_{C \to A}} = 0\]
This is because the volume is kept constant.
Thus the total work becomes:
\[ \Rightarrow W = {W_{A \to B}} + {W_{B \to C}} + {W_{C \to A}} = - 1200\]
\[ \Rightarrow 3325.6 + {W_{B \to C}} + 0 = - 1200\]
\[ \Rightarrow {W_{B \to C}} = - 1200 + ( - 3325.6) = - 4525.6J\]
Hence the work done by the gas in process B to C is −4525.6J.

Note:
While dealing with questions from thermodynamics make sure to put the correct signs. Heat released and work done by the system have negative signs. Heat absorbed and work done on the system have positive signs.
Also note that isothermal process, change in internal energy is zero. Adiabatic process change in heat is zero and isochoric process work done is zero.