
Considering Ellingham Diagram, which of the following metals can be used to reduce alumina?
A.Mg
B.Fe
C.Cu
D.Zn
Answer
489.9k+ views
2 likes
Hint: For this question we have to look into the Ellingham diagram. The element whose line will lie below the line for formation of alumina in the Ellingham diagram will be used for reduction. Alumina is aluminum oxide.
Complete step by step answer:
Ellingham diagram is a graph between
The Ellingham diagram is as follow:
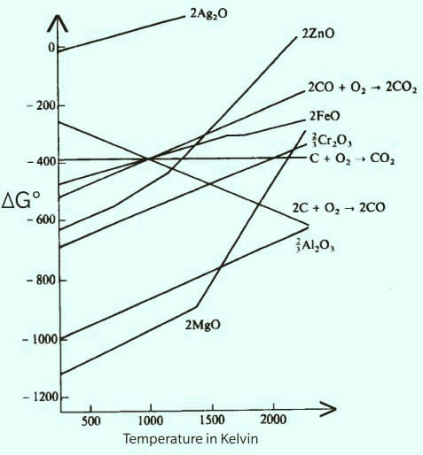
All the other metal lies above aluminium and hence less tendency to oxidize so cannot reduce alumina.
Hence the correct option is A.
Note:
In the Ellingham diagram the entropy slope of all the lines is generally positive. This is because gases are forming solid oxides, which is why the degree of randomness decreases and
Complete step by step answer:
Ellingham diagram is a graph between
The Ellingham diagram is as follow:

All the other metal lies above aluminium and hence less tendency to oxidize so cannot reduce alumina.
Hence the correct option is A.
Note:
In the Ellingham diagram the entropy slope of all the lines is generally positive. This is because gases are forming solid oxides, which is why the degree of randomness decreases and
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




