Question

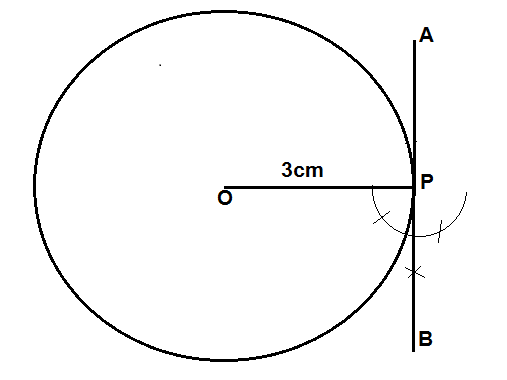
Construct a tangent at any point P on a circle of radius \[3{\text{ }}cm\].

Answer 1

Hint: In the above question, we have to construct a tangent on a circle of \[3{\text{ }}cm\]. After drawing the circle, you can draw the arc on both sides of the line, this will ease the extension of the tangent. Also, measure the angle so obtained after the bisection step with the help of the protractor, it should be exactly equal to 90 degrees.

The steps of construction are as given below:
$(i)$Mark a point O on the sheet of a paper.
$(ii)$Now, with O as centre and radius $r = 3cm$, draw a circle.
$(iii)$Now, take a point P on the circumference of the circle and join OP.
$(iv)$Take OP as base and P as vertex, draw a ray AB which is perpendicular to the base OP.
$(v)$This OP can be drawn with the help of a compass. Open the compass less than $3cm$and draw the two arcs.
$(vi)$Now with these arcs as centre, draw two other arcs such that the two newly formed arcs bisect each other.
$(vii)$Join this bisection point with the point P and extend the line.
$(viii)$Hence, the ray AB is the required tangent.

Note: Whenever we face such types of problems the key concept is to have an adequate knowledge of geometry. The marking of the arcs and the bisection point must be observed carefully. Join the points and extend the line with the help of a scale to maintain the precision of the diagram.