Question

Construct a triangle ABC in which BC = 7cm, $\angle B={{75}^{\circ }}$ and AB + AC = 13cm.

Answer 1

Hint: The concept applied in this question is the construction of triangles. Here, we have to write the whole steps and procedures in a well-defined manner. There are various methods for solving this question but here, it is written as "construct". Hence, we have to apply the construction steps method.
The approach is simple and easy to understand but if we don't know some basic theorems like "any point on a perpendicular bisector will be equidistant to (the same distance) the ends of the line segment it bisects", then it would be difficult to understand the steps properly.

Complete step by step answer:
Let’s move ahead to the solution. We have been given data as:
BC = 7cm, $\angle B={{75}^{\circ }}$ and AB + AC = 13cm
Steps of construction:
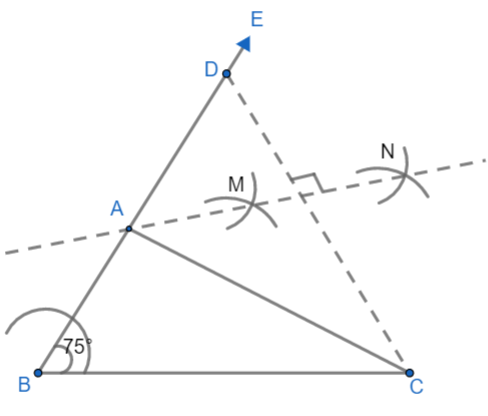
i) Draw the BC = 7cm as the base of the triangle.

ii) Now, we will place a compass at B and draw the semicircle of radius less than half the length of BC i.e. (less than $\dfrac{7}{2}=3.5cm$). Let BP as the radius.

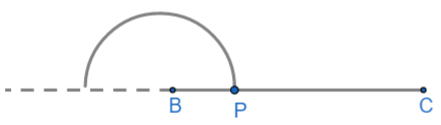
iii) Now, place the compass at P with the same radius and mark one arc on the semicircle. And then place the compass at the newly formed arc and draw another arc on the semicircle. The arc named as

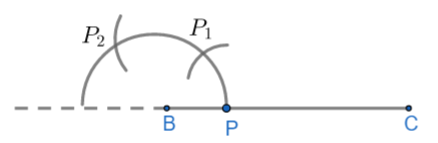
If we join $B{{P}_{1}}$ and $B{{P}_{2}}$ then we get $\angle {{P}_{1}}BC={{60}^{\circ }},\angle {{P}_{2}}BC={{120}^{\circ }}$

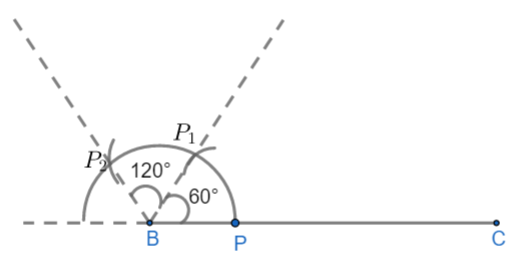
(iv) Now,
\[\begin{align}
  & \angle {{P}_{2}}B{{P}_{1}}=\angle {{P}_{2}}BC-\angle {{P}_{1}}BC \\
 & \Rightarrow {{120}^{\circ }}-{{60}^{\circ }} \\
 & \Rightarrow {{60}^{\circ }} \\
\end{align}\]
Then, find the angle bisector of angle $\angle {{P}_{2}}B{{P}_{1}}$ by following steps:
Cut an arc from point ${{P}_{2}}$ above as well as another arc from point ${{P}_{1}}$ above. They both will meet at a point. By joining this point and B we will get ${{90}^{\circ }}$.

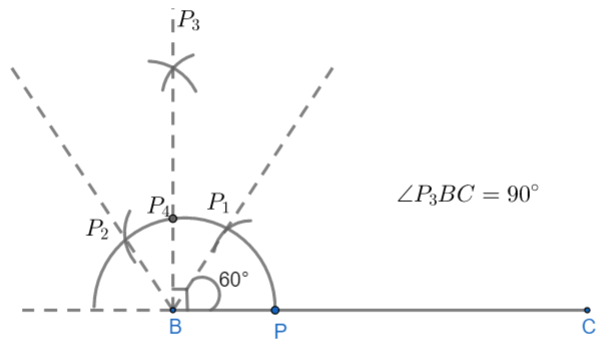
(v) Similarly, by following above steps we can find the angle bisector of \[\angle {{P}_{4}}B{{P}_{1}}\]

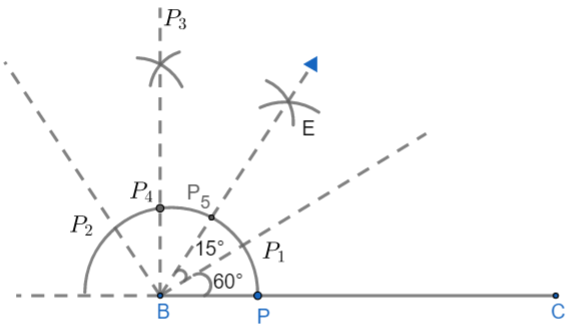
\[\begin{align}
  & \angle {{P}_{5}}B{{P}_{1}}=\dfrac{1}{2}\angle {{P}_{4}}B{{P}_{1}} \\
 & \Rightarrow \dfrac{1}{2}\times {{30}^{\circ }}={{15}^{\circ }} \\
\end{align}\]

Therefore, we have $\angle {{P}_{5}}BC={{15}^{\circ }}+{{60}^{\circ }}={{75}^{\circ }}$

Now, we have final figure as:

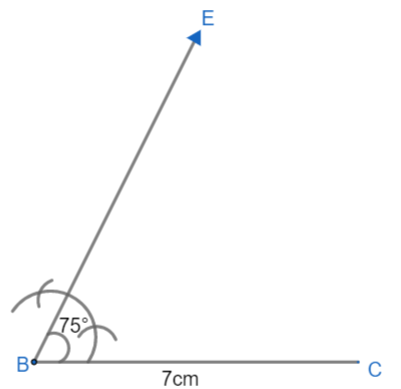
(vi) Now, from ray BE, cut off line segment BD, where BD=AB+BC=13cm. We will place a compass at B and taking 13cm in it, we will cut an arc such that it intersects BE at D.

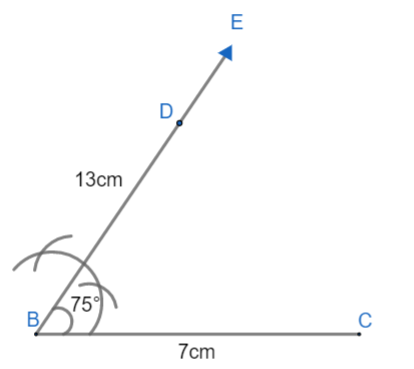
vii) Now, join the point D and C as dotted line.

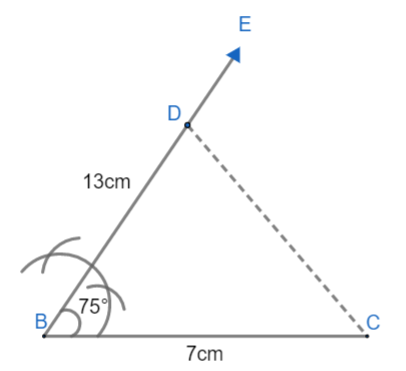
viii) Draw the perpendicular bisector of CD meeting BE at A. Open the compass more than half of the distance between C and D, and scribe arcs of the same radius centered at C and D.
Let these arcs meet at point M and N. Then, join the two points M and N and get required perpendicular bisector of CD.

Justification:
Since A lies on the perpendicular bisector of CD. Hence, AC = AD (we have already mentioned this theorem in hint).
Now,
\[\begin{align}
  & BD=13cm \\
 & BA+AD=13cm \\
 & BA+BC=13cm \\
\end{align}\]
Hence, triangle ABC is the required triangle.

Note:
 There would be some minor mistakes regarding angle accuracy while constructing with a protractor (because here we have to see whether the center point of the protractor matches with the point where we have to calculate the angle). In construction type questions, we have to set our hands with the compass (as sometimes in exams, the teacher doesn't allow protractor for angle measurement).