Question

Construct an angle of \[{240^0}\] using a compass and ruler.

Answer 1

Hint: Here in this question belongs to construction topic, we have to construct the angle of \[{240^0}\] it is a reflex angle which is greater than \[{180^0}\] and less than \[{360^0}\]. Construct by using a geometrical instrument like compass with provision of fitting a pencil and centi-meter scale or ruler.

Complete step by step answer:
In geometry, angle can be defined as the space formed by two rays meeting at a common point. Generally, an angle is represented by the symbol ‘\[\angle \]’ and measured in degrees \[\left( {^ \circ } \right)\]. Consider the question: construct an angle of \[{240^0}\] by using a compass and ruler. Given, angle \[{240^0}\] is greater than \[{180^ \circ }\] which means it is a reflex angle and lies between \[{180^0}\] and less than \[{360^0}\]. To construct the angle of \[\angle AOB = {240^ \circ }\] follow the below steps:

Steps of Construction:
1. Draw a line segment \[OA\] having a certain length.
2. a circle taking ‘\[O\]’ as centre and any radius i.e., \[OP\] (radius should be less than the length of \[OA\]).
3. Now, taking \[P\] as centre and with the same radius draw an arc and name the point where the arc intersects with the circle as ‘\[Q\]’ which makes an angle \[{60^ \circ }\] with line segment \[OA\]\[\therefore \angle AOQ = {60^ \circ }\].
4. Next, taking \[Q\] as centre and with the same radius draw an arc and name the point where the arc intersects with the circle as ‘\[R\]’ which makes an angle \[{120^ \circ }\] with line segment \[OA\]\[\therefore \angle AOR = {120^ \circ }\].
5. Again, taking \[R\] as centre and with the same radius draw an arc and name the point where the arc intersects with the circle as ‘\[S\]’ which makes an angle \[{180^ \circ }\] with line segment \[OA\]\[\therefore \angle AOS = {180^ \circ }\].
6. Similarly, taking \[S\] as centre and with the same radius draw an arc and name the point where the arc intersects with the circle as ‘\[B\]’ which makes an angle \[{240^ \circ }\] with line segment \[OA\] \[\therefore \angle AOB = {240^ \circ }\].

The required construction of angle \[\angle AOB = {240^ \circ }\] is:

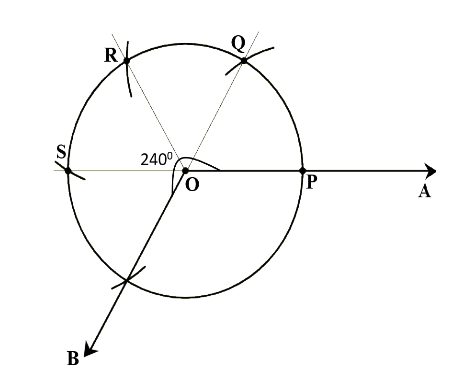
Note:When doing construction handling the instruments carefully, If the length of line segment is given in the question, we should draw a line of given length. Remember when making an arc between an angle or arc the radius will be the same which cannot be altered and angle between any two consecutive arcs is \[{60^ \circ }\]. If we can verify the construction easily by measuring the angle using an instrument called a protractor.