Question

Construct an isosceles trapezium ABCD in which AB is parallel to DC, AB = 11 cm, DC = 7 cm, AD = BC = 6 cm and calculate its area.

Answer 1

Hint- Do not directly use scale to draw any line, use compass to measure all the lengths from the scale and mark the points with the help of compass.

Complete step-by-step answer:

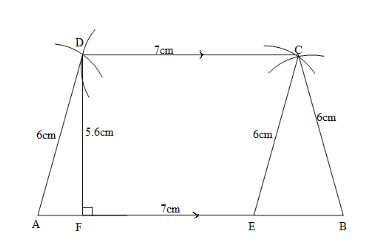
Given that: AB is parallel to DC, AB = 11 cm, DC = 7 cm, AD = BC = 6 cm.
Steps for construction
Step 1: Draw a rough diagram and mark the given measurements.
Step 2: Draw a line segment AB = 11 cm.
Step 3: Mark E on AB such that AE = 7 cm (since DC = 7 cm)
Step 4: With E and B as centers and (AD = EC = 6 cm) radius 6 cm draw two arcs. Let them cut at C.
Step 5: Join BC and EC.
Step 6 : With C and A as centers draw two arcs of radii 7 cm and 6 cm respectively and let them cut at D.
Step 7: Join AD and CD. ABCD is the required isosceles trapezium.
Step 8: From D draw $DF \bot AB$ and measure the length of DF. DF = h = 5.6 cm. AB = a = 11 cm and CD = b = 7 cm.


Calculation of area of the trapezium:
In the isosceles trapezium ABCD, a = 11 cm, b = 7 cm and h = 5.6 cm.
As we know that area of trapezium is given by:
${\text{Area}} = \dfrac{1}{2}\left( {{\text{sum of parallel sides}}} \right) \times \left( {{\text{distance between parallel sides}}} \right)$
So area of the given trapezium is given as:
${\text{Area}} = \dfrac{1}{2}\left( {AB + CD} \right) \times \left( {DF} \right)$
Let us substitute the values
$
   \Rightarrow {\text{Area}} = \dfrac{1}{2}\left( {11 + 7} \right) \times \left( {5.6} \right) \\
   \Rightarrow {\text{Area}} = \dfrac{1}{2}18 \times 5.6 \\
   \Rightarrow {\text{Area}} = 50.4c{m^2} \\
$
Hence, construction is done and the area of trapezium is 50.4 sq.cm.

Note- In order to solve these types of problems students must remember the complete steps in order to make no mistakes. Students must draw a reference line in order to start the problem and for uniqueness. The pencils must be sharp, compasses must be tight. Students must not disturb the setting of compass between the constructions.