Question

Construct rectangle JUMP with the following measurements. Find its area.
 $ UM = 3.6cm $ and $ MP = 4.6cm $ .

Answer 1

Hint: We are given the question we have to construct a rectangle with the given measurements. First we will choose a base for our rectangle. It can be any one of the given measurement in the question We will take one of them as the base, then with the help of protractor we will then construct a right angle with the line segment of the side equal to the other measurement and then keep on making the right angles with given measurements alternatively until we joint back with the given base. Also we have to calculate the area of the given rectangle measurements. The bigger value in the measurement will be considered as the length and the other one as the breadth , then we will use the formula stated below to find the area of the rectangle,
 $ Area = Length \times Breadth $
We will then have calculated the area as well as constructed the rectangle of the given measurements.

Complete step-by-step answer:
First steps for the construction of the rectangle.
We will choose $ MP $ as the base of the rectangle. We will first draw a line segment of the measurement $ 4.6 $ cm.
We will then make a line perpendicular (\[{90^ \circ }\]) to the base $ MP $ using a protractor. The perpendicular will be the second side of the rectangle its measure will be, $ UM = 3.6cm $ .
Then we will again make a line perpendicular (\[{90^ \circ }\]) to the line $ UM $ with the help of protractor , the measurement will be $ UJ = 4.6cm $
Now our three sides are done, then we will make a fourth line perpendicular (\[{90^ \circ }\]) to the line $ UJ $ with the measurement of $ 3.6cm $ using a protractor and scale. This perpendicular line will join the base $ MP $ at $ P $
Your diagram should look like the diagram below :

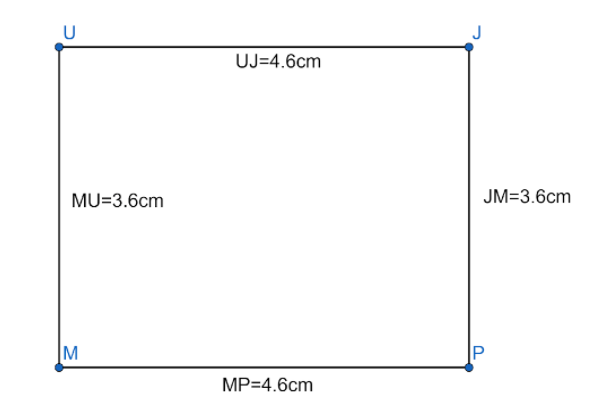
Now we will calculate the area of this rectangle.
The base $ MP $ will be the length and the perpendicular to the base, $ MU $ will be the breadth.
 $ Area = Length \times Breadth $
\[Area = 4.6 \times 3.6\]
 $ Area = 16.56{\text{ }}c{m^2} $
Which is the required answer.
So, the correct answer is “ $ Area = 16.56{\text{ }}c{m^2} $ ”.

Note: Remember the formula for the area of a rectangle,
 $ Area = Length \times Breadth $
Also remember that the rectangle has equal diagonals but those diagonals although bisecting each other are not perpendicular to each other. The perimeter of the rectangle is calculated using the formula,
 $ P = 2 \times (L + B) $
Where $ L $ is the length and the term $ B $ is the breadth of the rectangle. The angles between two adjacent sides of a rectangle is always the right angle.