
Construct the angle of
Answer
492.9k+ views
Hint: To construct the angle of
Complete step-by-step solution
We will follow the following steps to construct the angle of
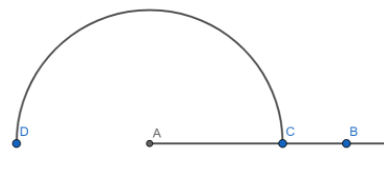
Step1: At first, we will first draw a ray OX and then put the pointed end of the compass at A and draw an arc of any radius which cuts AB at C.
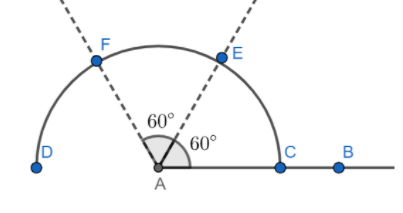
Step2: Now, we will mark the angle of
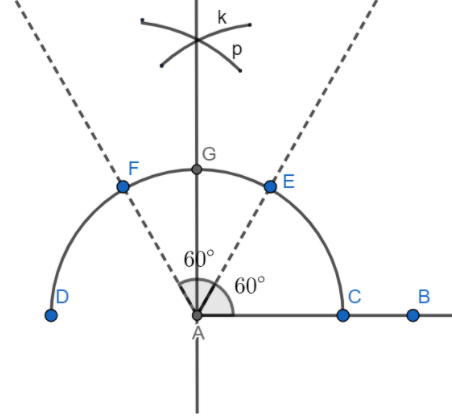
Step3: Now, we will bisect the angle
Step4: Now, at last we will see that
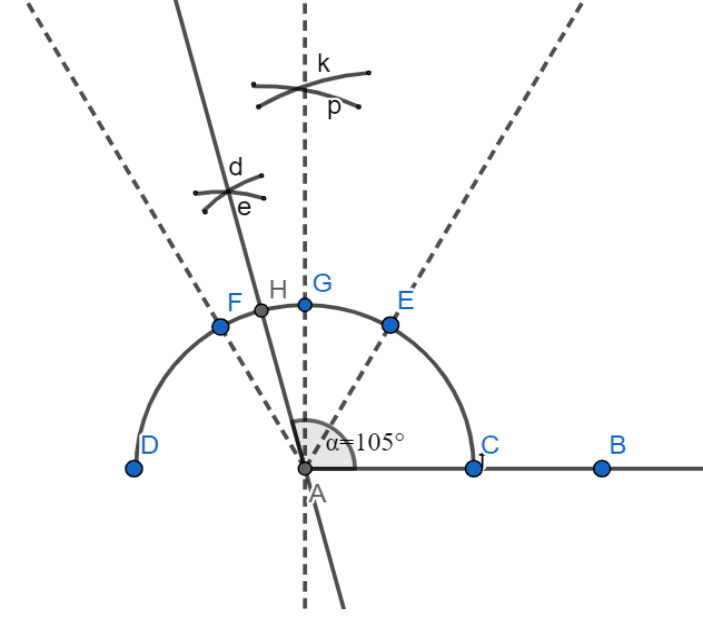
Note: Students are required to follow each step as stated above carefully otherwise they will not get the perfect angle and also note that we can draw the arc CEGFD of any radius. But, after that to mark angle
Complete step-by-step solution
We will follow the following steps to construct the angle of
Step1: At first, we will first draw a ray OX and then put the pointed end of the compass at A and draw an arc of any radius which cuts AB at C.

Step2: Now, we will mark the angle of

Step3: Now, we will bisect the angle

Step4: Now, at last we will see that

Note: Students are required to follow each step as stated above carefully otherwise they will not get the perfect angle and also note that we can draw the arc CEGFD of any radius. But, after that to mark angle
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples for herbs , shrubs , climbers , creepers

How many millions make a billion class 6 maths CBSE

Number of Prime between 1 to 100 is class 6 maths CBSE

Four bells toll together at 900am They toll after 7811 class 6 maths CBSE

Name the countries which are larger than India class 6 social science CBSE

1 lakh Thousand class 6 maths CBSE





