Question

Construct the following angles using set squares: 75 degree

Answer 1

Hint: Set squares are the thin flat triangular shaped scales having one angle of 90 degree. To draw an angle of 75 degree, the two different set squares having 30 degree and 45 degree are going to be used simultaneously. So that $({30^o} + {45^o})$ makes ${75^o}$

Complete step-by-step answer:
Step1 use both the set squares in combinations as ${45^o} + {30^o} = {75^o}$
Step 2 As there are two angles of 45 degree in 45 degree set square. It can be placed in two different ways and a ray can be drawn from either side measuring 45 degrees at one vertex.
Step 3 Place the \[{30^o}\] set square adjacent to\[{45^o}\]. Draw a ray from the same vertex along the edge of the second set square. The angle so obtained is of measure${75^o}$.

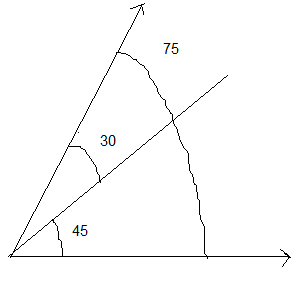
Step 4 Now the ray so obtained is the other aim of the angle required.
Note: The set squares are the two thin flat triangular scales. One having angles ${45^o},{45^o}\& {90^o}$ and other having angles ${60^o},{30^o}\& {90^o}$.
We constructed the angle of 75 degrees with the help of both set squares at the same time. The set squares are used to construct the angles having combinations of ${30^o},{60^o},{45^o},{75^o}\& {90^o}$.
The set squares are also used to draw parallel lines as well as the perpendicular lines. Set squares are also used to draw different types of geometrical shapes like squares, rectangles and certain types of triangles as well.