Question

How to convert 70 degrees into radians?

Answer 1

Hint: First understand the relation between the real number \[\pi \] and the angle corresponding to it in degrees. To do this, assume a circle of unit radius and use the relation: - \[\theta =\dfrac{l}{r}\] to establish the required relation between radian and degrees. Once the value of \[\pi \] radian is known in terms of degrees, find the value of 1 degree in terms of radian and multiply both the sides with 70 to get the answer.

Complete step-by-step solution:
Here, we have been provided with the angle \[{{70}^{\circ }}\] and we are asked to convert it into radian. But first we need to know the relation between radian and degrees.
Now, let us consider a circle with unit radius.

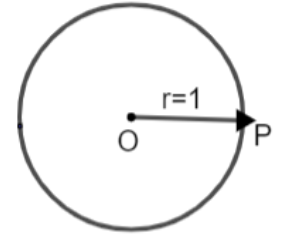
Consider a point P which starts moving on the circumference of this circle. We know that circumference of a circle is given as: - \[l=2\pi r\], here ‘l’ can be said as the length of the arc. Since, the radius is 1 unit, so we have,
\[\begin{align}
  & \Rightarrow l=2\pi \times 1 \\
 & \Rightarrow l=2\pi \\
\end{align}\]
Using the formula: - \[\theta =\dfrac{l}{r}\], we get,
\[\Rightarrow \theta =\dfrac{2\pi }{1}\]
\[\Rightarrow \theta =2\pi \] radian
Here, \[\theta \] represents the angle subtended by the initial and final position of the point P at the centre of the circle. Now, when this point P will return at the starting point then it will form an angle of \[2\pi \] radian but we know that it will form a complete angle, i.e., 360 degrees. So, we can relate the two units of measurement of angle as: -
\[\Rightarrow 2\pi \] radian = 360 degrees
\[\Rightarrow \pi \] radian = 180 degrees
Dividing both the sides with 180, we get,
\[\Rightarrow {{1}^{\circ }}=\left( \dfrac{\pi }{180} \right)\] radian
We have to find the value of \[{{70}^{\circ }}\] in terms of radian. So, multiplying both the sides with 70, we get,
\[\Rightarrow {{70}^{\circ }}=\left( 70\times \dfrac{\pi }{180} \right)\] radian
On simplifying the R.H.S., we get,
\[\Rightarrow {{70}^{\circ }}=\dfrac{7\pi }{18}\] radian
Hence, \[{{70}^{\circ }}\] measures \[\dfrac{7\pi }{18}\] radian.

Note: One may note that ‘\[\pi \]’ is a real number and its value is nearly 3.14. So, do not get confused. You don’t need to remember the derivation of the relationship between angle in radian and degrees but you need to remember the result, i.e., \[\pi \] radian = 180 degrees. Note that these notations are used in higher trigonometry instead of degrees. There is one more unit of angle measurement that is ‘Grad’ but very few books use this notation so we can ignore it.