
Why is the cosine of an obtuse angle negative?
Answer
391.5k+ views
Hint: An angle
The cosine of an obtuse angle is negative because of the range of the cosine function which is between 1 and -1. Therefore, when the cosine function completes its half cycle, it is at the middle of 1 and -1, that is 0. Thus, as a result when the cosine function reaches further the half cycle, it crosses 0 from the positive direction and becomes less than 0 i.e. negative.
Complete step-by-step answer:
The cosine functions, or
The cosine function is positive only in the first and the fourth quadrant.
This is why for an obtuse angle, where
Which is a negative real number because sine function positive for
For example,
That gives,
i.e.
We can also understand this by plotting the graph of a cosine function.
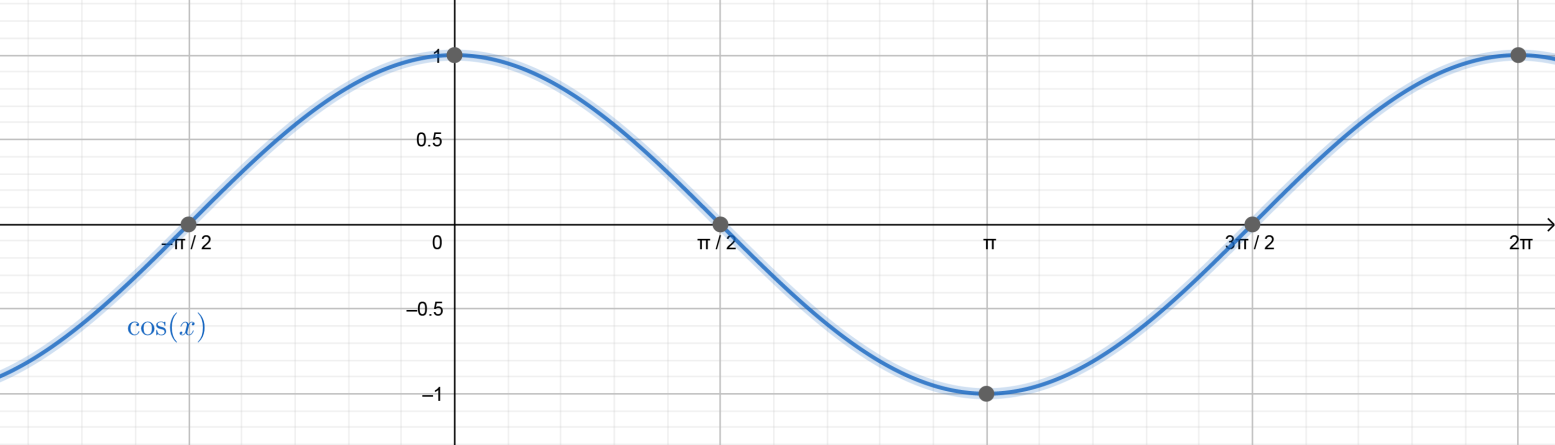
We can see that the cosine function is positive before
Note: In a right-triangle, cosine function is defined as the ratio of the length of the adjacent side to that of the longest side i.e. the hypotenuse. Suppose a triangle ABC is taken with AB as the hypotenuse and
The cosine function is one of the three main primary trigonometric functions (sine, cosine and tangent) and it is itself the complement of the sine function.
The cosine of an obtuse angle is negative because of the range of the cosine function which is between 1 and -1. Therefore, when the cosine function completes its half cycle, it is at the middle of 1 and -1, that is 0. Thus, as a result when the cosine function reaches further the half cycle, it crosses 0 from the positive direction and becomes less than 0 i.e. negative.
Complete step-by-step answer:
The cosine functions, or
The cosine function is positive only in the first and the fourth quadrant.
This is why for an obtuse angle, where
Which is a negative real number because sine function positive for
For example,
That gives,
i.e.
We can also understand this by plotting the graph of a cosine function.

We can see that the cosine function is positive before
Note: In a right-triangle, cosine function is defined as the ratio of the length of the adjacent side to that of the longest side i.e. the hypotenuse. Suppose a triangle ABC is taken with AB as the hypotenuse and
The cosine function is one of the three main primary trigonometric functions (sine, cosine and tangent) and it is itself the complement of the sine function.
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




