Question

How many cubes of 10 cm can be put in a cubical box of 1 m edge?

Answer 1

Hint: To find the number of cubes of 10 cm edge that could fit in a cube of 1 m edges, firstly find the volume of each cube in $c{{m}^{3}}$ by using the formula: $V={{a}^{3}}$, where a is the edge of the cube. Then, divide the volume of a cube of 1 m edges by the volume of a cube of 10 cm edge.

Complete step-by-step solution
We have:

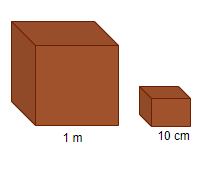
Side of the smaller cube: 10 cm
So, by using the formula of volume of cube $V={{a}^{3}}$, we get:
Volume of smaller cube ${{V}_{1}}={{10}^{3}}c{{m}^{3}}......(1)$
Also, side of larger cube: 1 m = 100 cm
So, by using the formula of volume of cube $V={{a}^{3}}$, we get:
Volume of larger cube ${{V}_{2}}={{100}^{3}}c{{m}^{3}}......(2)$
Now, we need to find the number of cubes of 10 cm edge that could fit in a cube of 1 m edges.
So, divide the volume of the larger cube by the volume of the smaller cube.
By substituting the values from equation (1) and equation (2), we get:
The number of smaller cubes that could fit the larger cube is
 $\begin{align}
  & \Rightarrow \dfrac{{{V}_{2}}}{{{V}_{1}}}=\dfrac{{{100}^{3}}}{{{10}^{3}}} \\
 & \Rightarrow \dfrac{{{10}^{3}}\times {{10}^{3}}}{{{10}^{3}}} \\
 & \Rightarrow 1000 \\
\end{align}$
Hence, 1000 cubes of 10 cm edge can fit inside a cubical box of 1 m edge.

Note: Remember, while finding the volume of each cube, units of measurements should be the same. As one cube edge is given in cm and another is given in m. So, convert anyone of them to get a standard unit while applying any mathematical identities.