Question

How many cyclic isomers does ${{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}$ have?

Answer 1

Hint: We are given a compound having molecular formula ${{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}$. To solve this we must know that the compounds having the same molecular formula but different structural formula are said to be isomers of each other and the phenomenon is known as isomerism.

 Complete answer:
We know that the compounds having the same molecular formula but different structural formulas are said to be isomers of each other and the phenomenon is known as isomerism.
We are given a compound having molecular formula ${{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}$.
Cyclic isomers are the compounds that have the same molecular formula but different cyclic or ring like structures.
We can draw structural isomers and geometrical isomers. In structural isomerism, the compounds have the same molecular formula but different structural formulas.
In geometrical isomerism, the compounds have the same molecular formula and structural formula but different arrangement of atoms or groups.
We can form three membered, four membered and five membered rings.
In the three membered ring we can attach the two methyl groups on one carbon side by side or join them as ethyl groups or we can attach two methyl groups on separate carbons.
Thus, the cyclic isomers of ${{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}$ are as follows:

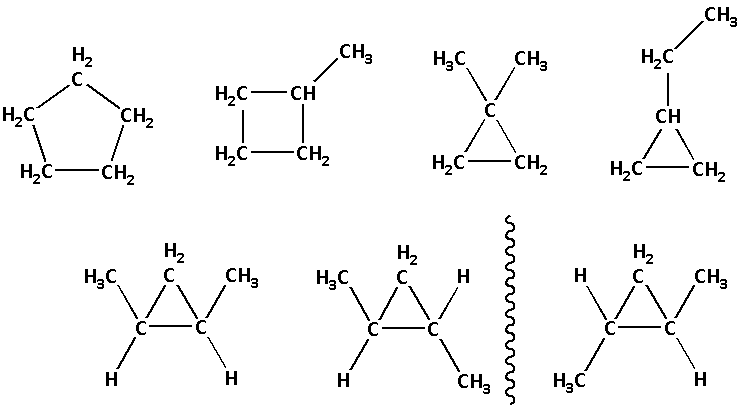
The two isomers are mirror images of each other and are known as enantiomers.
Thus, there are seven cyclic isomers of ${{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}$.

Note:The enantiomers in which the same groups are present on the same side are known as cis isomers and when the same groups are present on opposite side it is said to be trans isomer. Trans isomer is more stable than cis isomer.