Question

Define amplitude of wave.

Answer 1

Hint: A wave can take different forms such as elastic deformation, variation of pressure, and electric and magnetic intensity. There are various variables associated with a wave, be it mechanical or an electromagnetic wave. We will study about different types of amplitude associated with a simple wave or a sinusoidal wave.

Formula used:
Equation for a simple wave,
$x=A\sin \left[ w(t-K) \right]+b$

Complete step by step answer:
The amplitude of a wave is defined as the maximum amount of displacement of a particle on the medium from its rest or equilibrium position. Amplitude is the maximum distance or displacement moved by a particle on a wave from its equilibrium position.
There can be various types of amplitude associated with a wave.
Peak to peak amplitude: It is the change between peak, highest amplitude value, and the trough, lowest amplitude value of a wave.
Peak amplitude: in case of non-sinusoidal waves, the peak amplitude is the maximum absolute value of the difference from the reference point.
Semi-amplitude: Semi amplitude refers to half of the peak to peak amplitude.
Root mean square amplitude: it is defined as the square root of the mean value over time of the square of the vertical distance of particle in the graph from the rest state, that is, the RMS of AC form with no DC component.
Ambiguity: For an asymmetric wave, peak amplitude becomes ambiguous and is therefore known as Ambiguity.
Pulse amplitude: it is measured with respect to a specified reference and is modified by qualifiers, such as average or instantaneous peak or root mean square peak.
Representation of Amplitude of a wave and other variables associated with that wave:

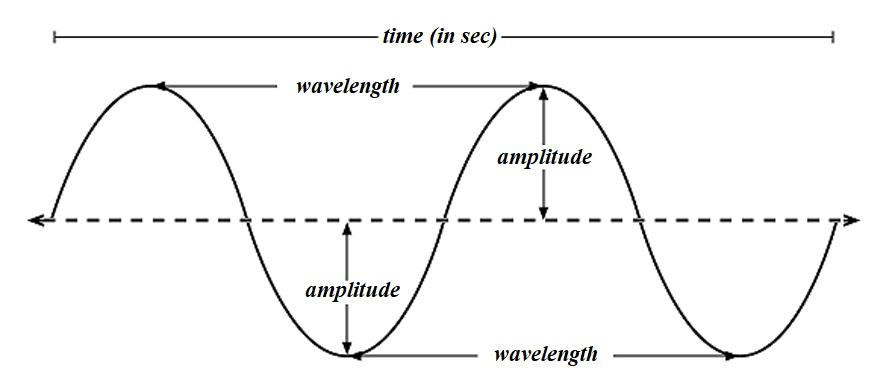
Equation for a simple wave,
$x=A\sin \left[ w(t-K) \right]+b$
$A$ is the amplitude, or peak amplitude
$x$ is the oscillating wave
$\omega $ is the angular frequency
$t$ is time
$K$ and $b$ are arbitrary constants, which represents time and displacement offsets respectively.

Note: While calculating the amplitude of a wave, distance is calculated taking the point of reference as the mean or equilibrium position of the particle. Extreme position can either be a Crust or a Trough. Also, waves are generated by vibrating sources; therefore, amplitude of wave is taken proportional to amplitude of the source.