Question

Define angle of friction.

Answer 1

Hint : The coefficient of friction between two surfaces is the tangent of the angle at which the object overcomes friction force and starts sliding. It can also be defined as the tangent of the angle of friction.

Complete step by step answer:
When a body experiences a friction force $ {F_f} $ , the angle of friction $ \theta $ can be seen in the diagram below:

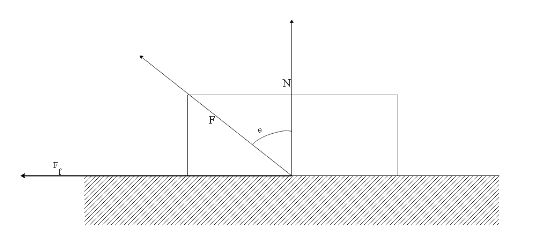
The coefficient of friction $ \mu $ is defined as the ratio of the friction force $ {F_f} $ to the normal force $ N $ . Hence, we can write:
 $ \mu = \dfrac{{{F_f}}}{N} $ ……………………..(1)
Now from the schematic diagram of the block, we can calculate the value of $ \tan \theta $ as the ratio of force in the horizontal direction to the ratio of the force in the vertical direction. Since the friction force $ {F_f} $ acts in the horizontal direction and the Normal force $ N $ acts in the vertical direction, we can write
 $ \tan \theta = \dfrac{{{F_f}}}{N} $ ……………………..(2)
Equalizing equation (1) and (2), we can write
 $ \tan \theta = \mu $
Hence the angle of friction is such that the tangent of the angle of friction is the coefficient of friction. If the external force overcomes the friction force acting on the object, then the object will start moving and the friction force will be constant irrespective of the movement of the block once it starts moving.

Note:
Since the coefficient friction of any surface can only lie between 0 and 1, the angle of friction can lie only between $ 0^\circ $ and $ 90^\circ $ . The angle of friction corresponds to the maximum static friction force between two surfaces and if the angle $ \theta $ between the block and the surface is less than the angle of friction, the block will start sliding on the surface.