
Define constant function. Also write its graph. Domain and range of function.
Answer
507.9k+ views
Hint: A function is a rule which relates the values of one variable quantity to the values of another variable quantity.
Complete step by step solution: A constant function is a function whose (output) value is the same for every input value.
For example, the function
Domain of function: The domain of a function is the complete set of possible values of the independent variable.
If
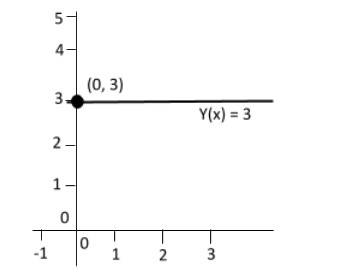
Range function: The range of a function is the complete set of all possible resulting values of the dependent variable of
For example:
Here: It is a set in the form of (
The values of
Then range
Note:
Complete step by step solution: A constant function is a function whose (output) value is the same for every input value.
For example, the function
Domain of function: The domain of a function is the complete set of possible values of the independent variable.
If

Range function: The range of a function is the complete set of all possible resulting values of the dependent variable of
For example:
Here: It is a set in the form of (
The values of
Then range
Note:
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




