Question

Define dispersion without deviation. Derive an expression for its essential conditions and resultant dispersion.

Answer 1

Hint: The splitting of light into its constituent colours is termed as dispersion. And the bend of the light rays from its original path is known as deviation. In order to achieve dispersion without deviation we need to set up two thin prisms. Hence find the mathematical expression for its dispersion.

Complete step by step answer:
When white light is passed through a glass prism it splits into its spectrum of colours i.e., in order violet, indigo, blue, green, yellow, orange and red (VIBGYOR) and this process of white light splitting into its constituent colours is termed as dispersion.
When light travels from one medium to another medium it deviates from its original path in the previous medium due to change in its velocity when travelling through the new medium. This is known as refraction of light.
DISPERSION WITHOUT DEVIATION:
In this phenomenon, two thin prisms are placed in contact in such a way that the two reflecting angles are revered with respect to each other. In this combination, the deviation for the mean colour produced by one prism is annulled by the deviation produced for that colour by another prism. However, after passing through the two prisms, there is some dispersion of light left, thus this kind of combination is used in direct vision spectroscopes.
C represents the crown glass and F represents the flint glass prism. They are joined with their bases opposite the angles A and A'. These prisms’ base opposite angles are so chosen that the resultant deviation produced by them is zero and there is only dispersion which is called dispersion without deviation.

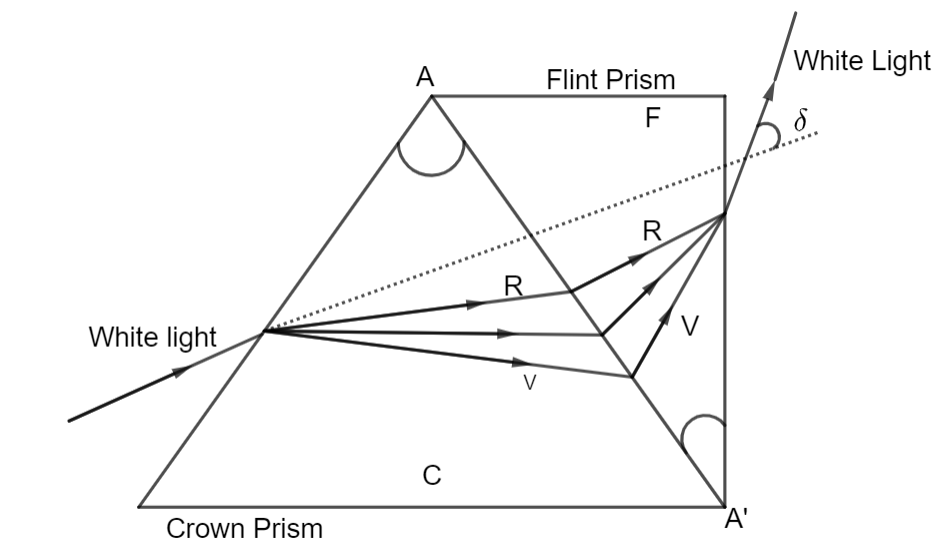
The essential condition for dispersion without deviation is that deviation produced by crown glass prism is equal to the deviation produced by flint glass prism.
Let the refractive indices of crown and flint glass prisms for mean ray are ​, then deviation of mean ray by crown prism.
${\delta }_{\gamma }=\left({\mu }_{\gamma }-1\right)A\cdots \cdots \cdots \cdots \left(1\right)$
Deviation of this ray by the flint prism
$\delta {}_{\gamma }^{\prime }=\left(\mu {}_{\gamma }^{\prime }-1\right)A^{\prime }\cdots \cdots \cdots \cdots \left(2\right)$
But resultant deviation is zero, thus
$\begin{array}{rl}& {\delta }_{\gamma }=-\delta {}_{\gamma }^{\prime }\\ & \text{Substituting values,}\\ & \left({\mu }_{\gamma }-1\right)A=-\left(\mu {}_{\gamma }^{\prime }-1\right)A^{\prime }\\ & \text{or }{A}^{\prime }=\left[{\displaystyle \frac{\left({\mu }_{\gamma }-1\right)}{\left(\mu {}_{\gamma }^{\prime }-1\right)}}\right]A\cdots \cdots \cdots \left(3\right)\end{array}$
The negative sign in the equation shows the direction i.e., that the refracting angles of both the prisms are in opposite directions.
Expression for resultant dispersions:
Let the refractive indices of crown for red and violet colour rays be respectively.
And similarly for the flint glass prisms let them be , respectively.
So, the angular dispersion for crown glass prism is:
$\begin{array}{rl}& {\theta }_1=({\mu }_v-{\mu }_R)A\cdots \cdots \cdots \left(4\right)\\ & \text{Similarly, angular dispersion for flint glass prism is:}\\ & {\theta }_2=(\mu {}_v^{\prime }-\mu {}_R^{\prime })A^{\prime }\cdots \cdots \left(5\right)\\ & \text{This resultant angular dispersion}\\ & \theta \text{ = }{\theta }_2-{\theta }_1\\ & \text{Substituting values from equation}\left(4\right)\text{and }\left(5\right),\text{we get:}\\ & \theta \text{ = }(\mu {}_v^{\prime }-\mu {}_R^{\prime })A^{\prime }-({\mu }_v-{\mu }_R)A\\ & \Rightarrow \theta =(\mu {}_v^{\prime }-\mu {}_R^{\prime })\left[{\displaystyle \frac{\left({\mu }_{\gamma }-1\right)}{\left(\mu {}_{\gamma }^{\prime }-1\right)}}\right]A-({\mu }_v-{\mu }_R)A\\ & \Rightarrow \theta =\left({\mu }_{\gamma }-1\right)A\left[{\displaystyle \frac{(\mu {}_v^{\prime }-\mu {}_R^{\prime })}{\left(\mu {}_{\gamma }^{\prime }-1\right)}}-{\displaystyle \frac{({\mu }_v-{\mu }_R)}{\left({\mu }_{\gamma }-1\right)}}\right]\\ & \Rightarrow \theta =\left({\mu }_{\gamma }-1\right)A\left({\omega }^{\prime }-\omega \right)\\ & \text{Where }\omega ={\displaystyle \frac{({\mu }_v-{\mu }_R)}{\left({\mu }_{\gamma }-1\right)}}\text{ and }{\omega }^{\prime }={\displaystyle \frac{(\mu {}_v^{\prime }-\mu {}_R^{\prime })}{\left(\mu {}_{\gamma }^{\prime }-1\right)}}\end{array}$

Note:
Students should make sure to use proper and distinguishable notations for the reflective indices. Solve the mathematical portion of the problem step by step to avoid any calculation error. Define every variable used to represent a physical quantity briefly.