
Define how you can draw tangent lines.
Answer
527.7k+ views
Hint: The equation which gives a linear relationship between two variables is termed to be as tangent lines. The instantaneous slope at some$ \left( {x,y} \right)$ coordinate on some function and the change of slope is being examined is equal to the slope of the equation which give a linear relationship between two variables.
Complete step-by-step answer:
To draw tangent lines, there are three main points to keep in mind.
We have to choose a point on the curve.
At that point on the curve, we have to put the straight edge.
Make sure that the point is equidistant from the curve on both sides of the point by adjusting the angles of the straight edge.
Let us draw a rough sketch of the graph so that the tangent lines become easier to understand.
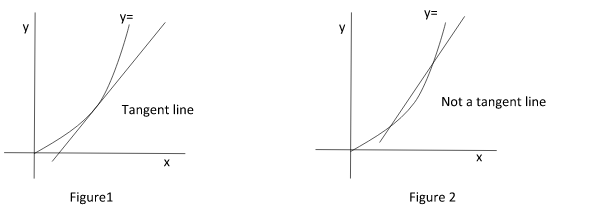
We have drawn a rough sketch of $y = {x^2}$ where$x \geqslant 0$ . In figure 1 , the line touches at one point of the curve that’s why it is a tangent line and in figure 2, the line touches two points of the curve so the straight line formed is not a tangent line.
Note: When we take a closer look to graph we can examine that on zooming it looks more and more linear as we keep zooming in and then, if we draw a straight line that traces appears to be a linear function on zooming and that straight line is the tangent line.
Complete step-by-step answer:
To draw tangent lines, there are three main points to keep in mind.
We have to choose a point on the curve.
At that point on the curve, we have to put the straight edge.
Make sure that the point is equidistant from the curve on both sides of the point by adjusting the angles of the straight edge.
Let us draw a rough sketch of the graph so that the tangent lines become easier to understand.
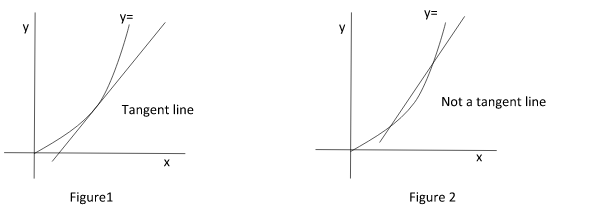
We have drawn a rough sketch of $y = {x^2}$ where$x \geqslant 0$ . In figure 1 , the line touches at one point of the curve that’s why it is a tangent line and in figure 2, the line touches two points of the curve so the straight line formed is not a tangent line.
Note: When we take a closer look to graph we can examine that on zooming it looks more and more linear as we keep zooming in and then, if we draw a straight line that traces appears to be a linear function on zooming and that straight line is the tangent line.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




