
Define many-one function. Give an example of many-one functions.
Answer
460.5k+ views
Hint: As we know that a function
With the help of this definition, we can give an example, consider elements of
Complete step-by-step answer:
Many-one function is defined as , A function
Let us consider an example ,
Let the domain or elements of
Let the co-domain or elements of
Such that
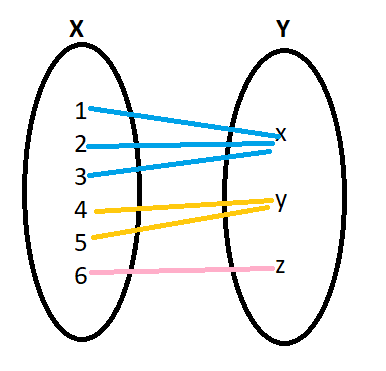
Here elements one , two and three all are connected with the same element that is
Note: Range is defined as the set of elements from
With the help of this definition, we can give an example, consider elements of
Complete step-by-step answer:
Many-one function is defined as , A function
Let us consider an example ,
Let the domain or elements of
Let the co-domain or elements of
Such that

Here elements one , two and three all are connected with the same element that is
Note: Range is defined as the set of elements from
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




