Question

 Define modulus function. Draw the graph of the modulus function and write its domain and range.

Answer 1

Hint: Here, first we have to define about the function, domain and range and then we should explain about the modulus function which is $f(x)=\left| x \right|=\left\{ \begin{align}
  & x,x\ge 0 \\
 & -x,x<0 \\
\end{align} \right.$ $\forall x\in \mathbb{R}$. Now for different values of $x$ find $y=f(x)$ to plot the graph and from the graph will get the idea about the domain and range of the function $f(x)$.

Complete step-by-step answer:
To define a modulus function first we should know about a function. A relation $f$ from a set A to a set B is said to be a function if every element of A has one and only one image in set B.
That is, for the notation $f:X\to Y$ means that $f$ is a function from $X$ to $Y$. $X$ is called the domain of $f$ and $Y$ is called the codomain of $f$. The set of all values of $f(x)$ taken together is called the range of $f$.
Range of $f$= $\left\{ y\in Y|y=f(x),\text{ for some }x\text{ in }X \right\}$
There are some specific types of functions. One of such function is the modulus function.
Now, we can define the modulus function. The modulus function is the real function $f:\mathbb{R}\to \mathbb{R}$ defined by:
$f(x)=\left| x \right|=\left\{ \begin{align}
  & x,x\ge 0 \\
 & -x,x<0 \\
\end{align} \right.$ $\forall x\in \mathbb{R}$.
Now, let us check $f(x)$ for different values of $x$.
Consider, $x=-1$ we have, $x<0,f(x)=-x$, then
$\begin{align}
  & y=f(-1) \\
 & y=-(-1) \\
 & y==1 \\
\end{align}$
Consider, $x=-2$ we have, $x<0,f(x)=-x$, then
$\begin{align}
  & y=f(-2) \\
 & y=-(-2) \\
 & y=2 \\
\end{align}$
Now, for $x=0$, we have, $x\ge 0$, so $f(x)=x$. Hence, we will get:
$\begin{align}
  & y=f(0) \\
 & y=0 \\
\end{align}$.
Consider, $x=1$, we have, $x>0$, so $f(x)=x$. Hence, we will get:
$\begin{align}
  & y=f(1) \\
 & y=1 \\
\end{align}$.
Consider, $x=2$, we have, $x>0$, so $f(x)=x$. Hence, we will get:
$\begin{align}
  & y=f(2) \\
 & y=2 \\
\end{align}$.
Now, let us plot the graph of modulus function.
Consider, some points to plot the graph.
First, for $x<0$, we have $f(x)=-x$. Now, consider two points:$$

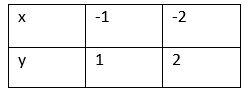
Now, consider for $x\ge 0$, we have $f(x)=x$. So, consider the points:

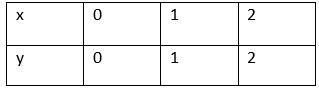
With these points we will get the graph as follows:

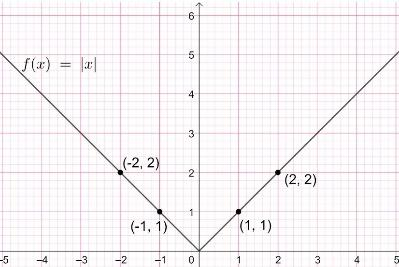
Now, from the graph, let us write the domain and range of the function $f(x)=|x|$.
Here, domain of $f$ = all values of real numbers, $\mathbb{R}$
Range of $f$ = all positive real numbers and zero.

Note: Here you have to split the function for $x<0$ and $x\ge 0$, to get a clear understanding. It is also helpful to plot the graph if you split the function, since the function is defined differently for both the cases.