
Define rectangular components of vectors.
Answer
497.4k+ views
Hint: The component form of a vector is the pair(ordered) which describes the changes that occur in the values of x-component and y-component.
Complete step-by-step answer:
A vector can be resolved into two components one along x-axis and the other along y-axis (if we plot the vector on the XY-plane).
The parts of a vector resolved into vertical and horizontal vectors are called rectangular components of the vector.
In other words, we can say that when the resolved components of a vector are mutually perpendicular i.e., they form an angle of
The horizontal component lies on the x-axis whereas the vertical component lies on the y-axis.
Rectangular components are perpendicular to each other.
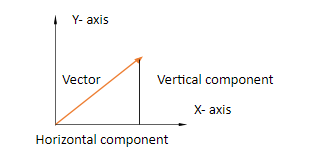
This figure shows both of the rectangular components of the vector. The orange line in the figure represents the vector while the black line represents the horizontal as well as the vertical components of the vector.
Note: The vector whose rectangular components are to be measured can lie in two dimensional plane (XY, YZ, XZ plane) as well as in three dimensional plane (XYZ-plane). The rectangular components of the vector will be three in number then. One component will be along the X-axis, the second will be along the Y-axis and the other third component will be along the Z-axis.
If it is not mentioned in the question to describe the rectangular component in which dimension, then write about both two dimensional and three dimensional as well.
Complete step-by-step answer:
A vector can be resolved into two components one along x-axis and the other along y-axis (if we plot the vector on the XY-plane).
The parts of a vector resolved into vertical and horizontal vectors are called rectangular components of the vector.
In other words, we can say that when the resolved components of a vector are mutually perpendicular i.e., they form an angle of
The horizontal component lies on the x-axis whereas the vertical component lies on the y-axis.
Rectangular components are perpendicular to each other.

This figure shows both of the rectangular components of the vector. The orange line in the figure represents the vector while the black line represents the horizontal as well as the vertical components of the vector.
Note: The vector whose rectangular components are to be measured can lie in two dimensional plane (XY, YZ, XZ plane) as well as in three dimensional plane (XYZ-plane). The rectangular components of the vector will be three in number then. One component will be along the X-axis, the second will be along the Y-axis and the other third component will be along the Z-axis.
If it is not mentioned in the question to describe the rectangular component in which dimension, then write about both two dimensional and three dimensional as well.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




