
Answer
468.3k+ views
Hint: The process of magnification can occur in lenses, telescopes, microscopes, and even in slide projectors. Simple magnifying lenses are biconvex -these lenses are thicker in the middle than at the sides.
Complete step by step solution:
The magnifying glass was one of the first-ever instruments which were used to magnify an object. Magnification relates to the scaling up of images to see the fine details by increasing the image resolution. There are mainly two types of magnification - linear and angular:
Linear or transverse magnification – This happens for real images, like those projected on screens.
Angular magnification – This sort of magnification occurs in optical instruments that contain an eyepiece. The size of the image is determined by the angle subtended by the object at the focal point.
The magnifying power of an instrument is the ratio between the angular size of the image, as seen through the instrument, and the angular size of the object as seen by the naked eye.
Magnifying power $\left( m \right)$ a microscope is defined as the ratio of the visual angle subtended by the image at the eye $\left( \beta \right)$ to the visual angle subtended by the object at the eye when placed a minimum of the distance of distinct vision$\left( \alpha \right).$
We can refer to following the figure for further understanding.
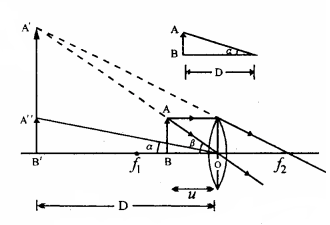
$\therefore {\text{m = }}\dfrac{\beta }{\alpha }$
Where $\beta $ is the visual angle of the image and $\alpha $ is the visual angle of the object, placed at the least distance of distinct vision.
As the angle $\alpha $ and$\beta $ are small therefore,
$\beta \approx \tan \beta $ and$\alpha \approx \tan \alpha $
$\therefore {\text{m = }}\dfrac{{\tan \alpha }}{{\tan \beta }}$
In $\Delta $ AOB, $\tan \beta = \dfrac{{{\text{AB}}}}{{{\text{OB}}}}$
And $\tan \alpha = \dfrac{{{\text{A''B'}}}}{{{\text{OB'}}}} = \dfrac{{{\text{AB}}}}{{{\text{OB'}}}}$ distinct vision.
$\Rightarrow m=\dfrac{tan \alpha}{tan \beta}$
In $\Delta AOB, tan \beta = \dfrac{AB}{OB}$
And, $tan \alpha=\dfrac{A’’B’}{OB’}=\dfrac{AB}{OB’}$ [Distinct vision]
$\Rightarrow =\dfrac{AB/OB}{AB/OB’}$
$\Rightarrow m=\dfrac{AB}{OB} \times \dfrac{OB’}{AB}=\dfrac{OB’}{AB}=\dfrac{D}{u}$
Now by using lens formula,
$\dfrac{1}{{\text{v}}} - \dfrac{1}{{\text{u}}} = \dfrac{1}{{\text{f}}}$
$ \Rightarrow \dfrac{1}{{{\text{( - D)}}}} - \dfrac{1}{{{\text{( - u)}}}} = \dfrac{1}{{\text{f}}}$
$ \Rightarrow \dfrac{1}{{\text{u}}} = \dfrac{{{\text{D + f}}}}{{{\text{Df}}}}$
$ \Rightarrow {\text{m = D}} \times \left( {\dfrac{{{\text{D + f}}}}{{{\text{Df}}}}} \right) = \left( {1 + \dfrac{{\text{D}}}{{\text{f}}}} \right)$
Note:
The mathematical formula for Magnifying Power, $M$ is
$M = \dfrac{D}{f}$ when the image forms at near point.
And also,
$M = 1 + \dfrac{D}{f}$ when the image forms at infinity.
Where $D$ is the least distance of distinct vision and is equal to $v$. $D$ being constant and the magnifying power depends upon the focal length of the lens. Smaller the focal length is going greater will be the magnifying power of the lens.
Complete step by step solution:
The magnifying glass was one of the first-ever instruments which were used to magnify an object. Magnification relates to the scaling up of images to see the fine details by increasing the image resolution. There are mainly two types of magnification - linear and angular:
Linear or transverse magnification – This happens for real images, like those projected on screens.
Angular magnification – This sort of magnification occurs in optical instruments that contain an eyepiece. The size of the image is determined by the angle subtended by the object at the focal point.
The magnifying power of an instrument is the ratio between the angular size of the image, as seen through the instrument, and the angular size of the object as seen by the naked eye.
Magnifying power $\left( m \right)$ a microscope is defined as the ratio of the visual angle subtended by the image at the eye $\left( \beta \right)$ to the visual angle subtended by the object at the eye when placed a minimum of the distance of distinct vision$\left( \alpha \right).$
We can refer to following the figure for further understanding.

$\therefore {\text{m = }}\dfrac{\beta }{\alpha }$
Where $\beta $ is the visual angle of the image and $\alpha $ is the visual angle of the object, placed at the least distance of distinct vision.
As the angle $\alpha $ and$\beta $ are small therefore,
$\beta \approx \tan \beta $ and$\alpha \approx \tan \alpha $
$\therefore {\text{m = }}\dfrac{{\tan \alpha }}{{\tan \beta }}$
In $\Delta $ AOB, $\tan \beta = \dfrac{{{\text{AB}}}}{{{\text{OB}}}}$
And $\tan \alpha = \dfrac{{{\text{A''B'}}}}{{{\text{OB'}}}} = \dfrac{{{\text{AB}}}}{{{\text{OB'}}}}$ distinct vision.
$\Rightarrow m=\dfrac{tan \alpha}{tan \beta}$
In $\Delta AOB, tan \beta = \dfrac{AB}{OB}$
And, $tan \alpha=\dfrac{A’’B’}{OB’}=\dfrac{AB}{OB’}$ [Distinct vision]
$\Rightarrow =\dfrac{AB/OB}{AB/OB’}$
$\Rightarrow m=\dfrac{AB}{OB} \times \dfrac{OB’}{AB}=\dfrac{OB’}{AB}=\dfrac{D}{u}$
Now by using lens formula,
$\dfrac{1}{{\text{v}}} - \dfrac{1}{{\text{u}}} = \dfrac{1}{{\text{f}}}$
$ \Rightarrow \dfrac{1}{{{\text{( - D)}}}} - \dfrac{1}{{{\text{( - u)}}}} = \dfrac{1}{{\text{f}}}$
$ \Rightarrow \dfrac{1}{{\text{u}}} = \dfrac{{{\text{D + f}}}}{{{\text{Df}}}}$
$ \Rightarrow {\text{m = D}} \times \left( {\dfrac{{{\text{D + f}}}}{{{\text{Df}}}}} \right) = \left( {1 + \dfrac{{\text{D}}}{{\text{f}}}} \right)$
Note:
The mathematical formula for Magnifying Power, $M$ is
$M = \dfrac{D}{f}$ when the image forms at near point.
And also,
$M = 1 + \dfrac{D}{f}$ when the image forms at infinity.
Where $D$ is the least distance of distinct vision and is equal to $v$. $D$ being constant and the magnifying power depends upon the focal length of the lens. Smaller the focal length is going greater will be the magnifying power of the lens.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




