
Define the terms vertically opposite angles, linear pair of angles, and adjacent angles with suitable diagrams.
Answer
507.3k+ views
Hint: Try to interpret the definitions of the terms mentioned in the question and represent them in the form of a diagram.
Complete step-by-step answer:
To start with the solution, we first try to describe the term vertically opposite angles. When two lines intersect at a point, then the pair of angles formed, which are opposite to each other, are called vertically opposite angles. They share the same vertex and are equal to mathematically. Vertically opposite angles can be represented by the diagram as:
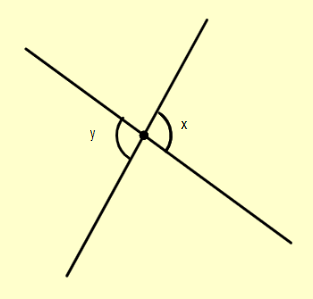
Now let’s move to adjacent angles. When two angles have a common side and a common corner but don’t overlap and are not the opposite, they are called adjacent angles. The diagram of adjacent angles is:
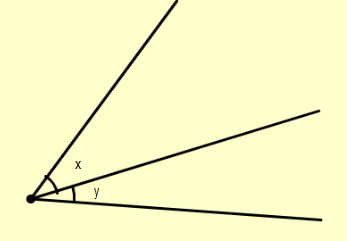
Now a linear pair of angles is defined as the pair of angles two angles that have a common side and a common corner but don’t overlap are not opposed to each other and whose sum is equal to
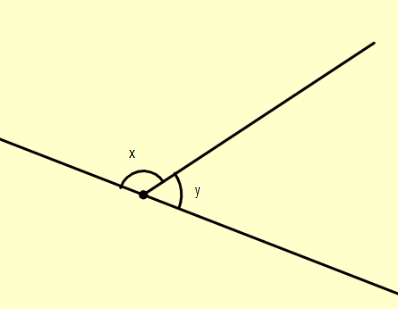
Note: It is very important to learn all the properties of vertically opposite angles and adjacent angles as they are often used. Also, a point of similarity of all the pair of angles talked about in the above question is that they share the same vertex and the same intersecting lines.
Complete step-by-step answer:
To start with the solution, we first try to describe the term vertically opposite angles. When two lines intersect at a point, then the pair of angles formed, which are opposite to each other, are called vertically opposite angles. They share the same vertex and are equal to mathematically. Vertically opposite angles can be represented by the diagram as:

Now let’s move to adjacent angles. When two angles have a common side and a common corner but don’t overlap and are not the opposite, they are called adjacent angles. The diagram of adjacent angles is:

Now a linear pair of angles is defined as the pair of angles two angles that have a common side and a common corner but don’t overlap are not opposed to each other and whose sum is equal to

Note: It is very important to learn all the properties of vertically opposite angles and adjacent angles as they are often used. Also, a point of similarity of all the pair of angles talked about in the above question is that they share the same vertex and the same intersecting lines.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




