
Define the word conjecture with an example.
Answer
495k+ views
Hint:First, we will define what conjecture is. Along with it, we will write a technical definition and also in simple terms. After that we will write an example, we will use or assume a recurring pattern we will write it for at least three variables and eventually generalize it.
Complete step by step answer:
So, in the question, we are asked to define the word conjecture. So, conjecture is a proposition which is consistent with known data but has neither been verified nor shown to be false. It is synonymous with the hypothesis. In simple terms, a statement that might be true, which is based on some research or reasoning, but is not proven.
We said that it is synonymous with hypothesis but it does not mean that they are similar conjecture is not stated in as formal, or testable, way. So, conjecture is like an educated guess, it is a mathematical statement that has not yet been rigorously proved. Conjectures arise when one notices a pattern that holds true for many cases. However, just because a pattern holds true for many cases does not mean that the pattern will hold true for all cases. Conjectures must be proved for mathematical observation to be fully accepted.
When a conjecture is rigorously proved, it becomes a theorem. A conjecture is an important step in problem-solving; it is not just a tool for professional mathematicians. In everyday problem solving, it is very rare that a problem's solution is immediately apparent. Instead, the problem-solving process involves analyzing the problem structure, examining cases, developing a conjecture about the solution, and then confirming that conjecture through proof.
Now, conjectures can be made by anyone, as long as one notices a consistent pattern.
Let’s take an example:
Let’s observe the following pattern:
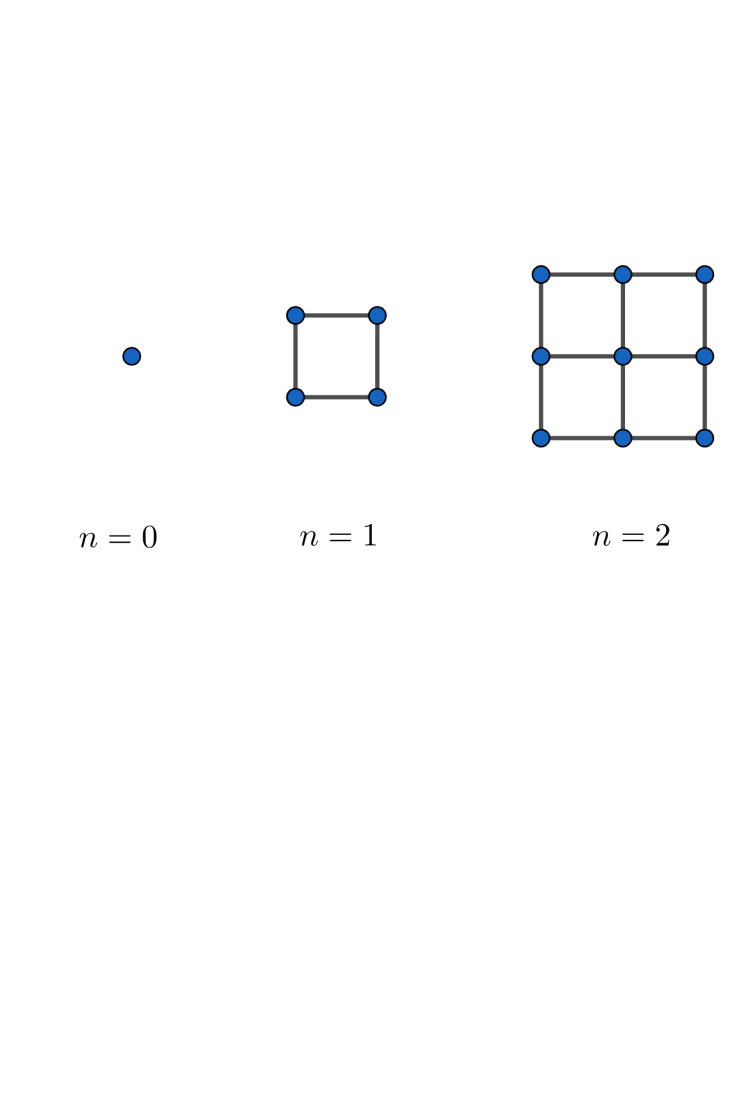
Now,
Let’s count the segments we have:
So, this observation could lead one to write a recurrence relation as follows:
Now, let’s see that the value of
We see that pattern appears to hold , so this gives enough information to write a conjecture. So our conjecture will be:
The number of segments connecting an
Note:
The last expression can be proven as follows:
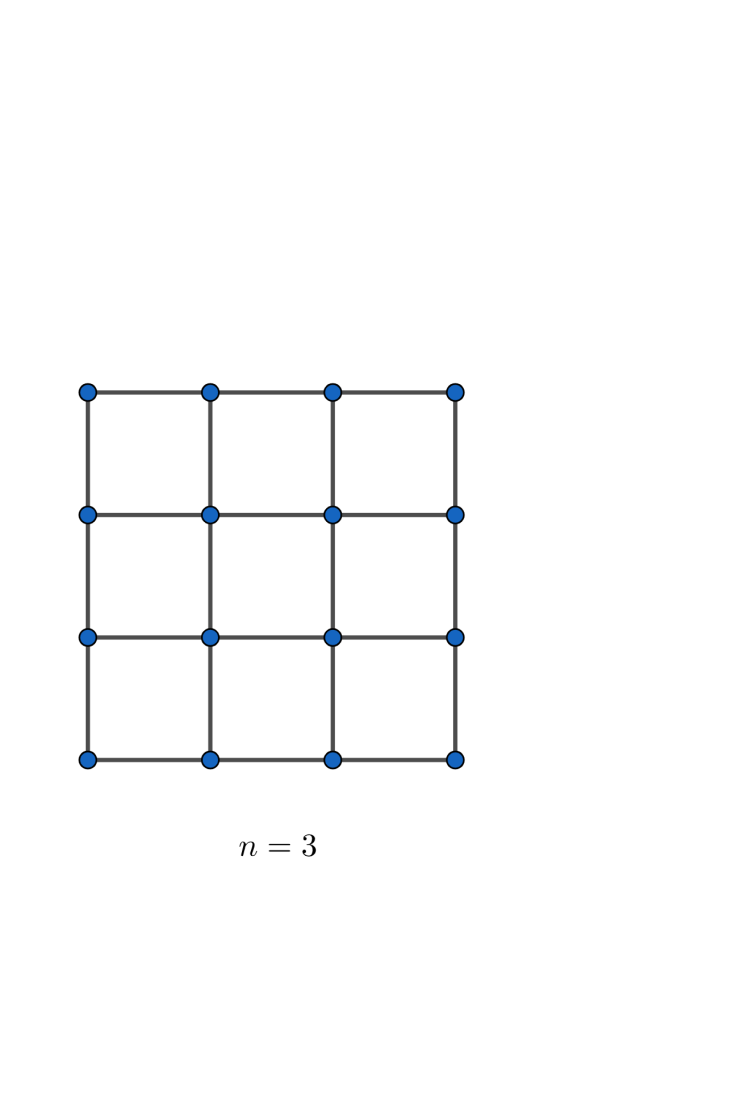
One could attempt to observe more cases in the sequence to see if any numerical pattern emerges. So, a better way to tackle these kinds of problems is to think more creatively about how the problem is structured. Let’s observe the same case for
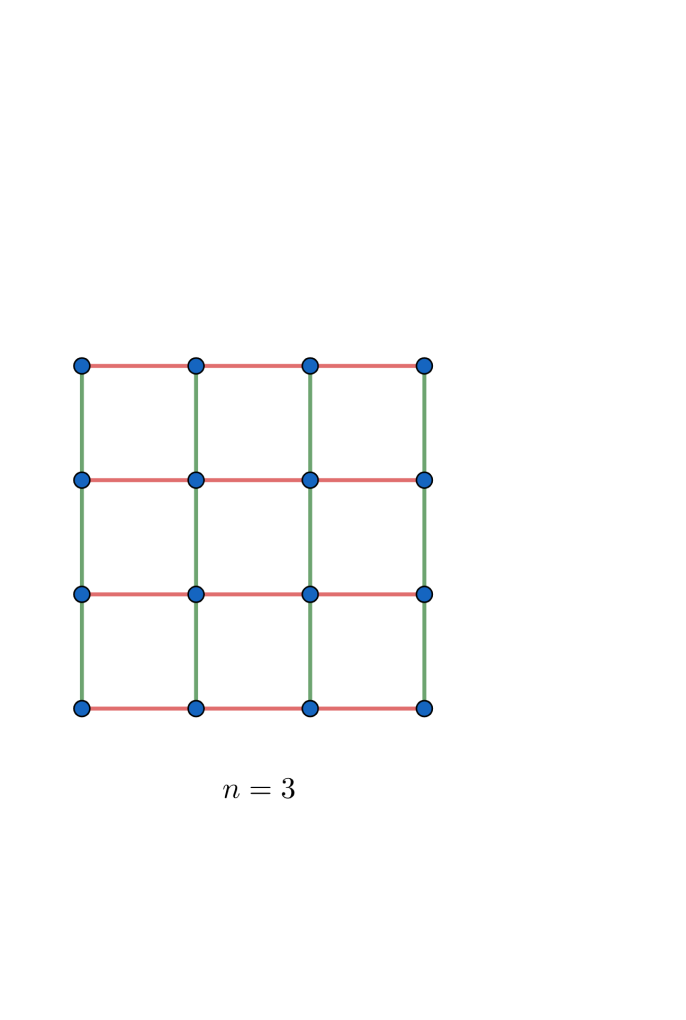
Notice that there are
Complete step by step answer:
So, in the question, we are asked to define the word conjecture. So, conjecture is a proposition which is consistent with known data but has neither been verified nor shown to be false. It is synonymous with the hypothesis. In simple terms, a statement that might be true, which is based on some research or reasoning, but is not proven.
We said that it is synonymous with hypothesis but it does not mean that they are similar conjecture is not stated in as formal, or testable, way. So, conjecture is like an educated guess, it is a mathematical statement that has not yet been rigorously proved. Conjectures arise when one notices a pattern that holds true for many cases. However, just because a pattern holds true for many cases does not mean that the pattern will hold true for all cases. Conjectures must be proved for mathematical observation to be fully accepted.
When a conjecture is rigorously proved, it becomes a theorem. A conjecture is an important step in problem-solving; it is not just a tool for professional mathematicians. In everyday problem solving, it is very rare that a problem's solution is immediately apparent. Instead, the problem-solving process involves analyzing the problem structure, examining cases, developing a conjecture about the solution, and then confirming that conjecture through proof.
Now, conjectures can be made by anyone, as long as one notices a consistent pattern.
Let’s take an example:
Let’s observe the following pattern:

Now,

Let’s count the segments we have:
So, this observation could lead one to write a recurrence relation as follows:
Now, let’s see that the value of
We see that pattern appears to hold , so this gives enough information to write a conjecture. So our conjecture will be:
The number of segments connecting an
Note:
The last expression can be proven as follows:
One could attempt to observe more cases in the sequence to see if any numerical pattern emerges. So, a better way to tackle these kinds of problems is to think more creatively about how the problem is structured. Let’s observe the same case for

Notice that there are
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




