
Answer
531k+ views
Hint: As, in the
Complete step-by-step answer:
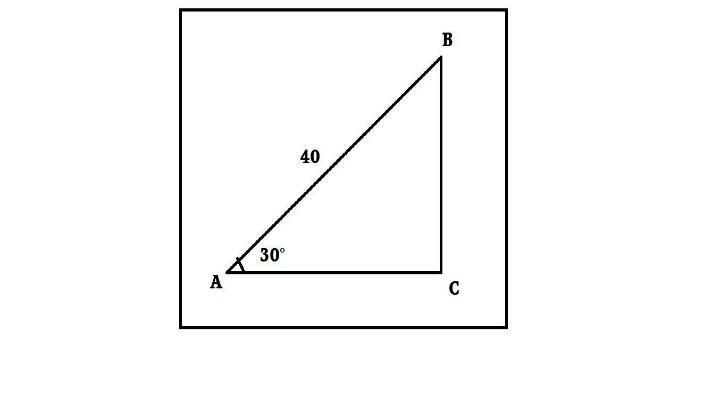
In the above
We know that
The angle that we are considering is
Also, we know that
Now, in the question, we are given that the length of side AB is given as AB = 40 units . So, substituting AB = 40 units in equation ( i ), we get:
Now, we know that in a right-angled triangle, if we know the length of any two sides of the triangle, we can find the third side using the Pythagorean Theorem.
Pythagoras theorem says that in a right-angled triangle,
Here, the unknown side is AC. So, according to Pythagoras Theorem,
Hence, by substituting the values of AB and BC, we get:
Therefore, the value of
Now, we have to find the angle B of the triangle ABC. Let us assume that the angle B =
Now, in the above
We know that
Here,
Hence, the value of
Note: Be careful while substituting the values of the trigonometric functions. Students generally get confused and make silly mistakes.
Complete step-by-step answer:

In the above
We know that
The angle that we are considering is
Also, we know that
Now, in the question, we are given that the length of side AB is given as AB = 40 units . So, substituting AB = 40 units in equation ( i ), we get:
Now, we know that in a right-angled triangle, if we know the length of any two sides of the triangle, we can find the third side using the Pythagorean Theorem.
Pythagoras theorem says that in a right-angled triangle,
Here, the unknown side is AC. So, according to Pythagoras Theorem,
Hence, by substituting the values of AB and BC, we get:
Therefore, the value of
Now, we have to find the angle B of the triangle ABC. Let us assume that the angle B =
Now, in the above
We know that
Here,
Hence, the value of
Note: Be careful while substituting the values of the trigonometric functions. Students generally get confused and make silly mistakes.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




