Question

Derive an expression for maximum height and range of an object in projectile motion.

Answer 1

Hint: As, here in this question, we need to derive the expression for maximum height and range of an object in projectile motion, we need to have a clear concept of the parabolic motion. We need to find out the trajectory or the path followed in a projectile motion. After that we need to use the components of the velocity vector in order to derive the expression for maximum height and range of an object in projectile motion. Also, we need to use Newton's equation of motion.

Complete answer:
Step one

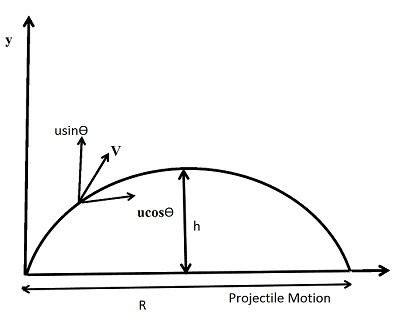
The horizontal component of velocity is given by, ${v_x} = u\cos \theta $
The vertical component of the velocity is given by, ${v_y} = u\sin \theta $
Let us assume that the body reaches the point P(x,y), after time $t$
Also, let us assume the maximum height to be H
Now, if we need to find the Horizontal distance, we can write the equation for it as,
$x = u\cos \theta t$ ………(i) As, distance = speed $ \times $time
Step two
Now, for maximum height of an object for projectile motion can be found by using third equation of motion, ${v^2} - {u^2} = 2as$
So, putting the values in the above equation, we get,
${o^2} - {(u\sin \theta )^2} = 2( - g)H$
$ \Rightarrow H = \dfrac{{ - {u^2}{{\sin }^2}\theta }}{{ - 2g}}$
$\therefore H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
Step three
Let the horizontal range be R
We know that time of flight, $T = \dfrac{{2u\sin \theta }}{g}$
Now, using equation (i) we can write,
$R = u\cos \theta T$
$ \Rightarrow R = u\cos \theta \times \dfrac{{2u\sin \theta }}{g}$
$\therefore R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Hence, the required value of maximum height is $\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ and the range is $\dfrac{{{u^2}\sin 2\theta }}{g}$.

Note:
We should not confuse time of maximum height with time of flight. Time of maximum height is the time when the object attains the maximum height and is given by $t = \dfrac{{u\sin \theta }}{g}$. Time of flight is the total time taken by the object to cover the total horizontal distance or in other words the time till when the object is in air and is given by $T = \dfrac{{2u\sin \theta }}{g}$.