Question

Derive an expression for the height in capillary rise between two parallel plates dipping in a liquid of density ‘$\sigma $’ separated by a distance ‘d’. The surface tension of the liquid is T.

Answer 1

Hint: We will calculate the pressure at two different heights in the capillary tube and then use it to derive an expression for the rise in height of liquid in the capillary tube. Also, since nothing is mentioned about the angle of contact of the liquid with the surface, we will take the angle of contact of the liquid and the surface as zero degree.

Complete answer:
Let us first try to understand our problem with the help of the following diagram:
                           

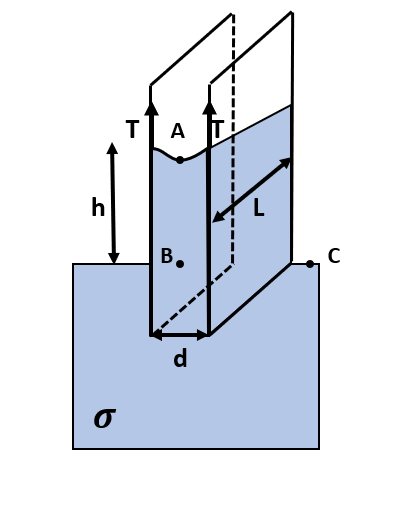
Here, we assume the rise in height of water in the capillary tube is ‘h’ and the length of the two sheets is equal to ‘L’. Also, let the net force due to surface tension be ‘${{F}_{T}}$’.
Also, since the angle of contact of the water and the capillary tube is zero, the force due to surface tension will act vertically upwards at the two ends.
Now, the force of surface tension at the contact of the lengths of the two sheets is equal to:
$\begin{align}
  & \Rightarrow {{F}_{T}}=2\times \left[ T\times L\times \cos \left( {{0}^{\circ }} \right) \right] \\
 & \Rightarrow {{F}_{T}}=2TL \\
\end{align}$
This force is acting upwards and should be balanced by the weight of liquid starting from point A to point B, where point B is at the same height as point C, that is, the top of the container.
This weight of water (say, W) will be equal to:
$\begin{align}
  & \Rightarrow W=\left( \text{Volume of water rises} \right)\times \left( \sigma \right)\times \left( g \right) \\
 & \Rightarrow W=\left( d\times l\times h \right)\times \left( \sigma \right)\times \left( g \right) \\
 & \Rightarrow W=dlh\sigma g \\
\end{align}$
Where, ‘g’ is the acceleration due to gravity.
Now, equating this weight of water with the force due to surface tension, we get:
$\begin{align}
  & \Rightarrow dLh\sigma g=2TL \\
 & \therefore h=\dfrac{2T}{\sigma dg} \\
\end{align}$
Hence, the expression for the height in capillary rise between two parallel plates dipping in a liquid of density ‘$\sigma $’ separated by a distance ‘d’ and having surface tension ‘T’ comes out to be, $h=\dfrac{2T}{\sigma dg}$.

Note:
While solving problems like this, we should be sure of our approach. Also, whenever the contact angle of a liquid and a solid is not mentioned in a problem, we will take it as zero. This is a standard assumption and can be applied to other questions also.