
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole.
Answer
591k+ views
Hint: To derive the expression for electric field due to an electric dipole, we will consider an electric dipole where two point charges are separated by a distance and then consider a point along the axial line of the dipole at certain distance from the center of the dipole for finding the field intensity. We will need to equate the electric field intensity due to two single charges on the point taken for finding the net intensity.
Complete step-by-step answer:
Let us consider $ AB $ to be an electric dipole of two point charges $ -q $ and $ +q $ separated by small distance $ 2d $ . Also we will take $ P $ as a point along the axial line of the dipole at a distance $ r $ from the midpoint of the dipole. i.e.
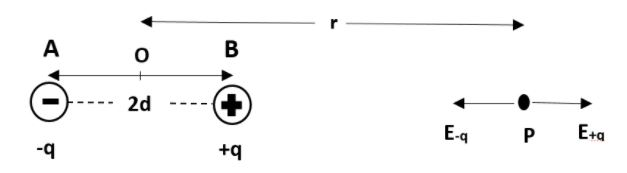
We know, electric field at any point due to a single charge $ q $ at a distance is given by, $ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{x}^{2}}} $
Where, $ {{\varepsilon }_{0}} $ is the permittivity of vacuum ( $ {{\varepsilon }_{0}}=8.85\times {{10}^{-12}} $ )
$ q $ is the charge
$ x $ is the distance of the point
Now, electric field at point $ P $ due to $ +q $ charge placed at $ B $ is given by,
$ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-d)}^{2}}} $ --- (along $ BP $ )
Also, electric field at point $ P $ due to $ -q $ charge placed at $ A $ is given by,
$ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{-q}{{{(r+d)}^{2}}} $ --- (along $ PA $ )
Therefore, the magnitude of resultant electric field acts in the direction of the vector with a greater magnitude. So, the resultant magnetic field will be,
$ E={{E}_{1}}+(-{{E}_{2}}) $
Putting the values, we will get
$ E=\left[ \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-d)}^{2}}}-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r+d)}^{2}}} \right] $ --- (along $ BP $ )
Simplifying further,
$ \begin{align}
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{1}{{{(r-d)}^{2}}}-\dfrac{1}{{{(r+d)}^{2}}} \right] \\
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{(r+d)}^{2}}-{{(r-d)}^{2}}}{{{(r-d)}^{2}}{{(r+d)}^{2}}} \right] \\
\end{align} $
Now, we can write $ {{(r+d)}^{2}}-{{(r-d)}^{2}}={{\left( {{r}^{2}}-{{d}^{2}} \right)}^{2}} $
So, we get
$ \begin{align}
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{\left( r \right)}^{2}}+{{\left( d \right)}^{2}}+2rd-{{\left( r \right)}^{2}}-{{\left( d \right)}^{2}}+2rd}{{{(r-d)}^{2}}{{(r+d)}^{2}}} \right] \\
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{4rd}{{{({{r}^{2}}-{{d}^{2}})}^{2}}} \right] \\
\end{align} $
Now, if the point $ P $ is far away from the dipole, then $ d\ll r $
So, the electric field will be,
$ E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{4rd}{{{({{r}^{2}})}^{2}}} \right]=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{4rd}{{{r}^{4}}}=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{4d}{{{r}^{3}}} $ --- (along $ BP $ )
Also, electric dipole moment $ p=q\times 2d $ , so the expression will now become,
$ E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{2\left( 2d \right)}{{{r}^{3}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}.\dfrac{2p}{{{r}^{3}}} $
$ E $ acts in the direction of dipole moment.
Note: We must know that whenever it is required to derive an expression, then always draw a rough sketch depicting a dipole and a point on the axial line. Another case for the electric field due to a dipole is on its equatorial line. We will need to resolve the electric field vectors for calculation in that case. As we are finding the field on the axial line, there is no need of resolving the field direction.
Complete step-by-step answer:
Let us consider $ AB $ to be an electric dipole of two point charges $ -q $ and $ +q $ separated by small distance $ 2d $ . Also we will take $ P $ as a point along the axial line of the dipole at a distance $ r $ from the midpoint of the dipole. i.e.

We know, electric field at any point due to a single charge $ q $ at a distance is given by, $ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{x}^{2}}} $
Where, $ {{\varepsilon }_{0}} $ is the permittivity of vacuum ( $ {{\varepsilon }_{0}}=8.85\times {{10}^{-12}} $ )
$ q $ is the charge
$ x $ is the distance of the point
Now, electric field at point $ P $ due to $ +q $ charge placed at $ B $ is given by,
$ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-d)}^{2}}} $ --- (along $ BP $ )
Also, electric field at point $ P $ due to $ -q $ charge placed at $ A $ is given by,
$ E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{-q}{{{(r+d)}^{2}}} $ --- (along $ PA $ )
Therefore, the magnitude of resultant electric field acts in the direction of the vector with a greater magnitude. So, the resultant magnetic field will be,
$ E={{E}_{1}}+(-{{E}_{2}}) $
Putting the values, we will get
$ E=\left[ \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-d)}^{2}}}-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r+d)}^{2}}} \right] $ --- (along $ BP $ )
Simplifying further,
$ \begin{align}
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{1}{{{(r-d)}^{2}}}-\dfrac{1}{{{(r+d)}^{2}}} \right] \\
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{(r+d)}^{2}}-{{(r-d)}^{2}}}{{{(r-d)}^{2}}{{(r+d)}^{2}}} \right] \\
\end{align} $
Now, we can write $ {{(r+d)}^{2}}-{{(r-d)}^{2}}={{\left( {{r}^{2}}-{{d}^{2}} \right)}^{2}} $
So, we get
$ \begin{align}
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{\left( r \right)}^{2}}+{{\left( d \right)}^{2}}+2rd-{{\left( r \right)}^{2}}-{{\left( d \right)}^{2}}+2rd}{{{(r-d)}^{2}}{{(r+d)}^{2}}} \right] \\
& E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{4rd}{{{({{r}^{2}}-{{d}^{2}})}^{2}}} \right] \\
\end{align} $
Now, if the point $ P $ is far away from the dipole, then $ d\ll r $
So, the electric field will be,
$ E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{4rd}{{{({{r}^{2}})}^{2}}} \right]=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{4rd}{{{r}^{4}}}=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{4d}{{{r}^{3}}} $ --- (along $ BP $ )
Also, electric dipole moment $ p=q\times 2d $ , so the expression will now become,
$ E=\dfrac{q}{4\pi {{\varepsilon }_{0}}}.\dfrac{2\left( 2d \right)}{{{r}^{3}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}.\dfrac{2p}{{{r}^{3}}} $
$ E $ acts in the direction of dipole moment.
Note: We must know that whenever it is required to derive an expression, then always draw a rough sketch depicting a dipole and a point on the axial line. Another case for the electric field due to a dipole is on its equatorial line. We will need to resolve the electric field vectors for calculation in that case. As we are finding the field on the axial line, there is no need of resolving the field direction.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




