Question

Derive an expression for work done in adiabatic expansion.

Answer 1

Hint: Consider an isolated non-conducting cylinder, with a non-conducting piston and then pull the piston by a little amount outward which will cause a change in the physical conditions of the gas, and then find the work done to make the change.

Complete step by step solution:
Suppose we have a one-gram molecule of a perfect gas which has been enclosed in a non-conducting cylinder having a non-conducting piston. The gas will expand, if we move the piston slowly outwards and hence will do some work without any energy being supplied from outside and thus adiabatic expansion will take place. And since the energy hasn’t been used from outside, the temperature of the gas in the cylinder will fall.

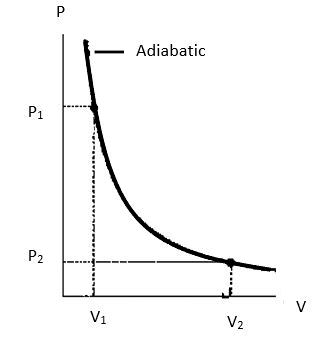
Let us say the initial temperature, pressure and volume of the cylinder be $T_1$, $P_1$ and $V_1$ and in its final state be $T_2$, $P_2$ and $V_2$.
Now, let the cross-sectional area of the piston be A and we move the piston through a small distance dx which makes the gas expand by a volume of dV. And for small expansion, the pressure change will be almost the same, say P.
Now, for an adiabatic change $PV^{\gamma}=K$ (constant}
Therefore, $P=\dfrac{K}{V^{\gamma}}$
Thus, the work done, $W= \int_{V_1}^{V_2}PdV$
$\implies W=\int_{V_1}^{V_2}\dfrac{K}{V^{\gamma}}dV=K\int_{V_1}^{V_2}V^{-\gamma}dV$
$\therefore, W=K\left|\dfrac{V^{1-\gamma}}{1-\gamma}\right|=\dfrac{K}{1-\gamma}({V_2}^{1-\gamma}-{V_1}^{1-\gamma})$
Since, in adiabatic expansion, we know that
${P_1}{V_1}^{\gamma}={P_2}{V_2}^{\gamma}=k$
Thus, $W=\left(\dfrac{1}{1-\gamma}\right)({P_2}{V_2}^{\gamma}{V_2}^{1-\gamma}-{P_1}{V_1}^{\gamma}{V_1}^{1-\gamma})$
$\implies W=\left[\dfrac{1}{1-\gamma}\right][{P_2}{V_2}-{P_1}{V_1}]$
 Using, $PV=RT$, we can also write the work done as,
$W=\left[\dfrac{R}{1-\gamma}\right][T_2 - T_1]$
This is the equation for work done in adiabatic expansion.

Note: We can also derive the expression for the work done by graphical method using a PV curve for the change in pressure and volume during an adiabatic expansion, then the area under the curve will give us the required work done.