Question

Derive the expression for capacitance of parallel plate capacitor.

Answer 1

Hint: Find the total electric field due to both the plates of the capacitor. Use it to find the potential difference between them. Divide total charge by potential difference to get the capacitance.

Formula used: $C=\dfrac{Q}{V}$
Here
     C is capacitance
     Q is charge
     V is potential difference

Complete step by step solution:

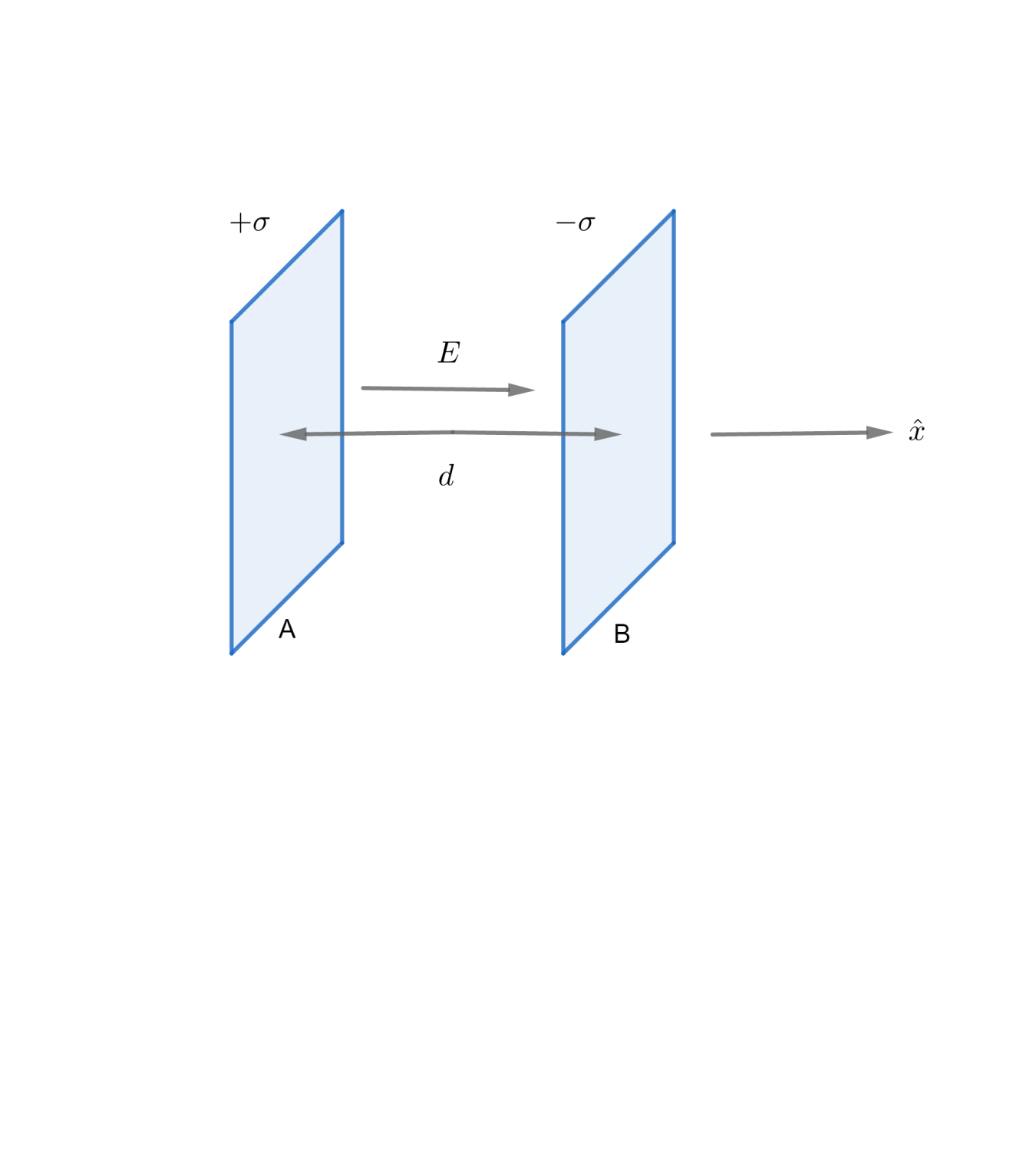
Let the two plates be parallel be each other each carrying a surface charge density $+\sigma $ and $-\sigma $ respectively. $A$ is the area of the plates and $d$ is the separation between them.
The electric field of a thin charged plate is given by \[E=\dfrac{\sigma }{2{{\epsilon }_{0}}}\] and is directed normally outwards from the plate. The total electric field between the two plates is given as

     $\begin{align}
  & \overrightarrow{E}={{\overrightarrow{E}}_{A}}+{{\overrightarrow{E}}_{B}} \\
 & \overrightarrow{E}=\dfrac{+\sigma }{2{{\epsilon }_{0}}}(+\hat{x})+\dfrac{-\sigma }{2{{\epsilon }_{0}}}(-\hat{x})=\dfrac{\sigma }{{{\epsilon }_{0}}}\hat{x} \\
 & E=|\overrightarrow{E}|=\dfrac{\sigma }{{{\epsilon }_{0}}}=\dfrac{Q/A}{{{\epsilon }_{0}}}=\dfrac{Q}{A{{\epsilon }_{0}}} \\
\end{align}$
The potential difference between the two plates is
     $V=E\times d=\dfrac{Qd}{A{{\epsilon }_{0}}}$
The capacitance is
     $C=\dfrac{Q}{V}=\dfrac{A{{\epsilon }_{0}}}{d}$

Additional information: If a dielectric is introduced between the two plates, then the capacitance of the arrangement will increase $k$ times where $k$ is the dielectric constant of the medium. Capacitors are used to store charge and energy. They are used in digital circuits to store and restore information in case of power failure. They are used to supply pulsed power in particle accelerators and fusion research. They are also used as components in oscillators.

Note: If both the plates carry the same charge (either both positive or both negative), then the net electric field between them will be zero.