
Derive the expression for the scalar product of two vectors in terms of their scalar component. Give two examples of scalar products.
Answer
453.9k+ views
1 likes
Hint: A vector quantity is a physical quantity which has both direction and magnitude and a scalar quantity is a physical quantity which has only magnitude and not direction. The dot product or the scalar product is defined as the product of two vectors to obtain a scalar quantity.
Complete answer:
A vector quantity can be defined as the quantity which has both the direction and the magnitude. A scalar quantity can be defined as the quantity which has only magnitude but not directions.
Scalar product can be defined as the product of the two vectors to form a scalar, whose value is the product of the magnitude of the vectors and the cosine of the angle between the vectors.
Now, we can simply define the scalar product of two vectors by taking the component of one vector in the direction of the other vector and then multiplying it to the magnitude of the other vector. The scalar product of the two vectors is also called the inner product or the dot product.
Consider two vectors
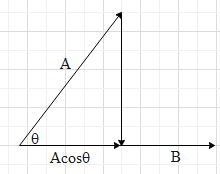
Where, A is the magnitude of the vector
The work done is given by the dot product of the force and the distance covered by the object. It is an example of a scalar product.
The power can be found as the dot product of the force and the velocity of the object. This is another example of dot product.
Hence the question is answered.
Note: We also have another type of multiplication which is called the vector multiplication. A vector multiplication is a multiplication where we will obtain a vector after multiplying two vector quantities. It is expressed as,
Complete answer:
A vector quantity can be defined as the quantity which has both the direction and the magnitude. A scalar quantity can be defined as the quantity which has only magnitude but not directions.
Scalar product can be defined as the product of the two vectors to form a scalar, whose value is the product of the magnitude of the vectors and the cosine of the angle between the vectors.
Now, we can simply define the scalar product of two vectors by taking the component of one vector in the direction of the other vector and then multiplying it to the magnitude of the other vector. The scalar product of the two vectors is also called the inner product or the dot product.
Consider two vectors

Where, A is the magnitude of the vector
The work done is given by the dot product of the force and the distance covered by the object. It is an example of a scalar product.
The power can be found as the dot product of the force and the velocity of the object. This is another example of dot product.
Hence the question is answered.
Note: We also have another type of multiplication which is called the vector multiplication. A vector multiplication is a multiplication where we will obtain a vector after multiplying two vector quantities. It is expressed as,
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




