Question

Derive the first equation of motion by graphical method.

Answer 1

Hint So to derive the first equation of motion we can derive it by using the graph made for the velocity-time relation and it will be for the moving object which having $u$as the initial velocity, $v$ as a final velocity, and $a$as an acceleration of the body.

Complete Step By Step Solution

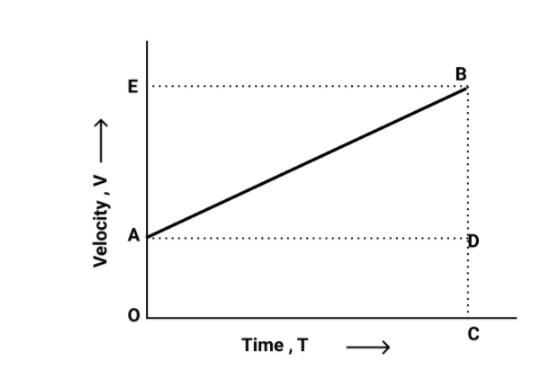
So from the above graph, we see that,
From \[A\]to $B$in the time duration $t$ at a uniform rate, there is a change in the velocity of the body. Here, at the time $t$ the total time will be $OC$ and the final velocity will be $BC$.
From $B$ to $OC$ a perpendicular will be drawn and similarly from $A$to $D$ parallel line will be drawn and one another there is the line which is perpendicular drawn from $B$ to $OE$ and this line is represented in the form of dotted lines.
So, from the graph we get,
Initial velocity, $u = OA$
Final velocity, $v = BC$
And as we know that, from the graph
$BC = BD + DC$
Therefore, we can say that
$BC = BD + DC$
And also since, $DC = OA$
Therefore,
$BC = BD + OA$
So from the above, we can write it as
$ \Rightarrow V = BD + u$ , since$OA = u$.
So let the above equation be ${1^{st}}$the equation.
Now we see that the acceleration $a$will be equal to the slope of the velocity-time graph.
Therefore,
$a = $Slope of line $AB$
And also
$ \Rightarrow a = \dfrac{{BD}}{{AD}}$
Since we see from the graph that the$AD = AC = t$, therefore the above equation will look like
$BD = at$, let make this equation the second equation.
So by combining the two-equation we have got, we will get
$v = u + at$
The above is the first equation of motion.

Note So we see the derivation of the first equation of motion which is derived by the use of the graphical method. There are two other methods with which it can be derived, the first one is by using the algebraic method and the other one is by using the calculus method.