Question

Derive the formula for moment of inertia of a hoop with axis across the diameter.

Answer 1

Hint: To solve the questions related to moment of inertia of continuous distribution we consider the moment of inertia for an infinitesimal part of the body having infinitesimal mass and then integrate it for the whole body. To solve the integral, we consider the relation of infinitesimal mass with the mass of the whole body and try to convert the whole integral into known parameters.

Formula used:
Moment of inertia for continuous body is given by formula,
$I = \int {dm \times {r_ \bot }} $
Where $dm$ denotes the mass of the considered infinitesimal element and ${r_ \bot }$ is the perpendicular distance of the element from the axis of rotation.

Complete step by step answer:
Let us take the total mass of the hoop be $M$ and radius be $r$. Now, consider a small element of mass dm at distance $r'$ from the axis of rotation as shown in the figure.

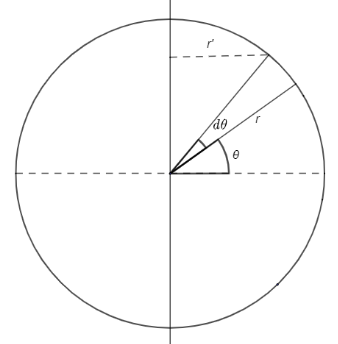
Moment of inertia for this small element is $ = dm \times r'$
Now, we will integrate it to get the moment of inertia for the whole hoop.
\[I = \int {dm \times r'} \]
We will try to simplify the integral using-
$dm = \dfrac{M}{{2\pi }}d\theta $
Also, $r' = r\cos \theta $
Now, substitute these values in the integral and integrate-
$I = \int\limits_0^{2\pi } {\dfrac{M}{{2\pi }}} d\theta \times {(r\cos \theta )^2}$
$\Rightarrow I = \dfrac{M}{{2\pi }}{r^2}\int\limits_0^{2\pi } {{{\cos }^2}} \theta d\theta $
We know that, ${\cos ^2}\theta = \dfrac{{1 + \cos 2\theta }}{2}$, substitute this in previous equation and solve-
\[I = \dfrac{M}{{2\pi }}{r^2}\int\limits_0^{2\pi } {\dfrac{{1 + \cos 2\theta }}{2}} d\theta\\
\Rightarrow I= \dfrac{M}{{2\pi }}{r^2}{\left[ {\dfrac{\theta }{2} + \dfrac{{\sin 2\theta }}{4}} \right]_0}^{2\pi }\]
On putting the limits, we get-
$I = \dfrac{M}{{2\pi }}{r^2}[(\pi + 0) - (0 + 0)] \\
\therefore I = \dfrac{{M{r^2}}}{2} \\ $
Hence the required moment of inertia of a hoop with axis across the diameter is $\dfrac{{M{r^2}}}{2}$.

Note: This approach of considering the moment of inertia for a small element and then integrating it for the whole body is the most general approach and can be used for any continuous distribution. However, this same derivation can be done using the perpendicular axis theorem if students remember the moment of inertia for the hoop about an axis passing through the centre of the hoop and perpendicular to the plane. That approach would come handy in competitive exams where time is a constraint.