Question

Describe the displacement method to determine focal length of Convex lens under the following headings:-
(i) Ray Diagram
(ii) Formula Derivation
(iii) Why should the distance between two pins be greater than 4f?

Answer 1

Hint: In this figure, the same lens is used to experiment and shifting the lens in two different positions we get the focused image of the object. Then apply lens formula and calculate the value of u and from that calculate the value of v . Now find the value of d y putting the value of u and v we get the focal length of the lens.

Complete step-by-step solution:
This is the required set up of the experiment.

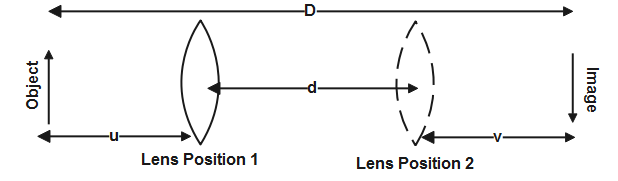
 i)Ray diagram for displacement method to determine focal length -

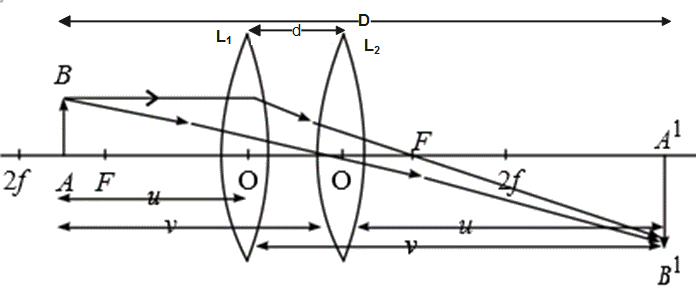
Initially the lens L1 is placed at position 1 closer to the object AB and its position is so adjusted so that we get clear image A1B1 on the screen. The position of the lens and the distance between the object and the image is marked and noted.
Keeping the same distance between the object and image, the lens is now moved to a new position towards the screen in new position 2 and in this position lens is adjusted till a clear image is obtained on the screen. This position of the lens and distance between the object and image is marked and noted.
(ii) Formula Derivation : -Let us assume the distance between object and image is D.
Let us assume the distance between two positions of the lens is d.
This displacement method is based on principle on the reversibility of light, if the direction of a ray of light is reversed, it will follow the same path as that of the original path.
Hence, the distance of the object from the lens and that of the image from the lens can be interchanged and we still get a focused image.
We therefore get the two positions of the lens for getting a clear focused image of an object with the same distance between the object and image on both positions of object and image. In other words, the distance between the object and the lens in the first position is the same as the distance between the image and the lens in the second position and also, the distance between the image and the lens in the first position is the same as the distance between the object and lens in the second position.
Distance between object and lens is u.
Distance between image and lens is v.
Let focal length of lens f.
Apply Lens formula,
\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\](Equation 1)
According to figure ,
\[v=D-u\] (Equation 2)
Put in equation 1 ,
\[\dfrac{1}{f}=\dfrac{1}{D-u}-\dfrac{1}{u}\]
\[\Rightarrow \dfrac{1}{f}=\dfrac{u-(D-u)}{(D-u)u}\]
\[\Rightarrow \dfrac{1}{f}=\dfrac{-D}{(D-u)u}\]
\[\Rightarrow Du-{{u}^{2}}=-fD\]
\[\therefore {{u}^{2}}-Du+fD=0\]
This is the required quadratic equation. Solving this equation by quadratic formula, we get
\[\therefore \]\[u=\dfrac{D\pm \sqrt{{{D}^{2}}-4fD}}{2}\]
(iii) Case :-I When \[D=4f\]then \[u=\dfrac{D}{2}=2f\].
In a convex lens when the object is a 2f then image is also formed on 2f.So ,we get only one position of the lens to get the focused image. So this is not valid for the displacement method.
Case :- II When \[D<4f\] , then we get an imaginary value of u which is not valid for the displacement method so distance can never be less than 4f.
Case:- III When \[D>4f\]then we find two different values of u .
\[u=\dfrac{D+\sqrt{{{D}^{2}}-4fD}}{2},\dfrac{D-\sqrt{{{D}^{2}}-4fD}}{2}\]
Put this value of u in equation 2 and we get two different values of v.
\[v=\dfrac{D-\sqrt{{{D}^{2}}-4fD}}{2},\dfrac{D+\sqrt{{{D}^{2}}-4fD}}{2}\]
Now we calculate the value of Displacement d, this value of d can be written from both positions of lens.
Since , \[d=v\sim u\]
\[\therefore d=\sqrt{{{D}^{2}}-4fD}\]
Now solve this equation to find the focal length of the lens.
Square on both sides, we get
 \[\Rightarrow {{d}^{2}}={{D}^{2}}-4fD\]
 \[\Rightarrow 4fD={{D}^{2}}-{{d}^{2}}\]
\[\therefore f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}\]
This is the required value of focal length for convex lens by displacement method. This value can be achieved when \[D> 4f\].

Note: Convex lens is also called a converging lens because it converges all parallel light rays falling on the lens at a single point called focus and distance between focus and lens is always defined as focal length. The sign convention of focal length for convex lenses is always taken as negative and that for concave lens it is taken as positive.