
Answer
443.1k+ views
Hint: Here, we are required to find the vertices of the triangle graphically whose equations of the sides are given. We will find the points which are satisfying each equation respectively. Plotting these points on a graph and joining them together, will give us the required lines showing these equations; which will be intersecting to form the required triangle. We will mark the coordinates of the triangle formed, hence, determining the required vertices of the triangle.
Complete step-by-step answer:
According to the question,
The given equations of the sides of a triangle are: $2y - x = 8$, $5y - x = 14$ and $y - 2x = 1$.
Now, for the equation; $2y - x = 8$
This can also be written as:
$x = 2y - 8$
Hence, for $y = 4$
$x = 2\left( 4 \right) - 8 = 0$
And for $y = 2$
$x = 2\left( 2 \right) - 8 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
Now, for the equation $5y - x = 14$
This can also be written as:
$x = 5y - 14$
Hence, for $y = 3$
$x = 5\left( 3 \right) - 14 = 1$
And for $y = 2$
$x = 5\left( 2 \right) - 14 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
Also, for the equation $y - 2x = 1$
This can also be written as:
$y = 2x + 1$
Hence, for $x = 0$
$y = 2\left( 0 \right) + 1 = 1$
And for $x = - 1$
$y = 2\left( { - 1} \right) + 1 = - 2 + 1 = - 1$
Therefore, we can draw the table, showing the points satisfying this equation:
Now, we will draw a graph showing all the given equations by plotting the above points from their respective tables and joining them to form a triangle.
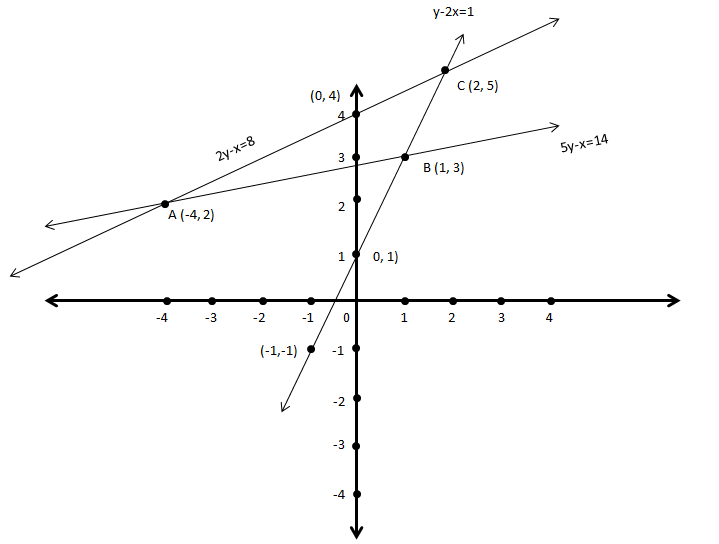
From the above graph; which is showing the lines representing the given equations, we can see that these lines are intersecting with each other to form a triangle.
We have marked the intersecting points forming the triangle $ABC$ as $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$ respectively. Hence, the required coordinates of the vertices of the triangle formed by the given equations are $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$.
Therefore, this is the required answer.
Note: In this question, we have found the points satisfying each equation and then we plotted them on a graph to find the vertices of the required triangle. An alternate way of finding the vertices when the equations of the sides are given is that, we can eliminate the three equations by taking two of them at a time and hence, finding the coordinates of the vertices simultaneously. When the vertices are found, we can plot them directly on a graph and join them together to get the required triangle. But since, in this question we were required to determine graphically the vertices of a triangle, hence, we followed the above method. If it was not asked specifically to determine the vertices graphically, then we could have used this alternate method.
Complete step-by-step answer:
According to the question,
The given equations of the sides of a triangle are: $2y - x = 8$, $5y - x = 14$ and $y - 2x = 1$.
Now, for the equation; $2y - x = 8$
This can also be written as:
$x = 2y - 8$
Hence, for $y = 4$
$x = 2\left( 4 \right) - 8 = 0$
And for $y = 2$
$x = 2\left( 2 \right) - 8 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -4 | 0 |
| y | 2 | 4 |
Now, for the equation $5y - x = 14$
This can also be written as:
$x = 5y - 14$
Hence, for $y = 3$
$x = 5\left( 3 \right) - 14 = 1$
And for $y = 2$
$x = 5\left( 2 \right) - 14 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -4 | 1 |
| y | 2 | 3 |
Also, for the equation $y - 2x = 1$
This can also be written as:
$y = 2x + 1$
Hence, for $x = 0$
$y = 2\left( 0 \right) + 1 = 1$
And for $x = - 1$
$y = 2\left( { - 1} \right) + 1 = - 2 + 1 = - 1$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -1 | 0 |
| y | -1 | 1 |
Now, we will draw a graph showing all the given equations by plotting the above points from their respective tables and joining them to form a triangle.

From the above graph; which is showing the lines representing the given equations, we can see that these lines are intersecting with each other to form a triangle.
We have marked the intersecting points forming the triangle $ABC$ as $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$ respectively. Hence, the required coordinates of the vertices of the triangle formed by the given equations are $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$.
Therefore, this is the required answer.
Note: In this question, we have found the points satisfying each equation and then we plotted them on a graph to find the vertices of the required triangle. An alternate way of finding the vertices when the equations of the sides are given is that, we can eliminate the three equations by taking two of them at a time and hence, finding the coordinates of the vertices simultaneously. When the vertices are found, we can plot them directly on a graph and join them together to get the required triangle. But since, in this question we were required to determine graphically the vertices of a triangle, hence, we followed the above method. If it was not asked specifically to determine the vertices graphically, then we could have used this alternate method.
Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE

Fill in the blanks with suitable articles Tribune is class 10 english CBSE

Rearrange the following words and phrases to form a class 10 english CBSE

Select the opposite of the given word Permit aGive class 10 english CBSE

Fill in the blank with the most appropriate option class 10 english CBSE

Some places have oneline notices Which option is a class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Which are the Top 10 Largest Countries of the World?

What is the definite integral of zero a constant b class 12 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Define the term system surroundings open system closed class 11 chemistry CBSE

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




