Question

Determine the current through zener diode for the circuit shown in the figure: (Given zener diode breakdown voltage ${V_z} = 5.6V$

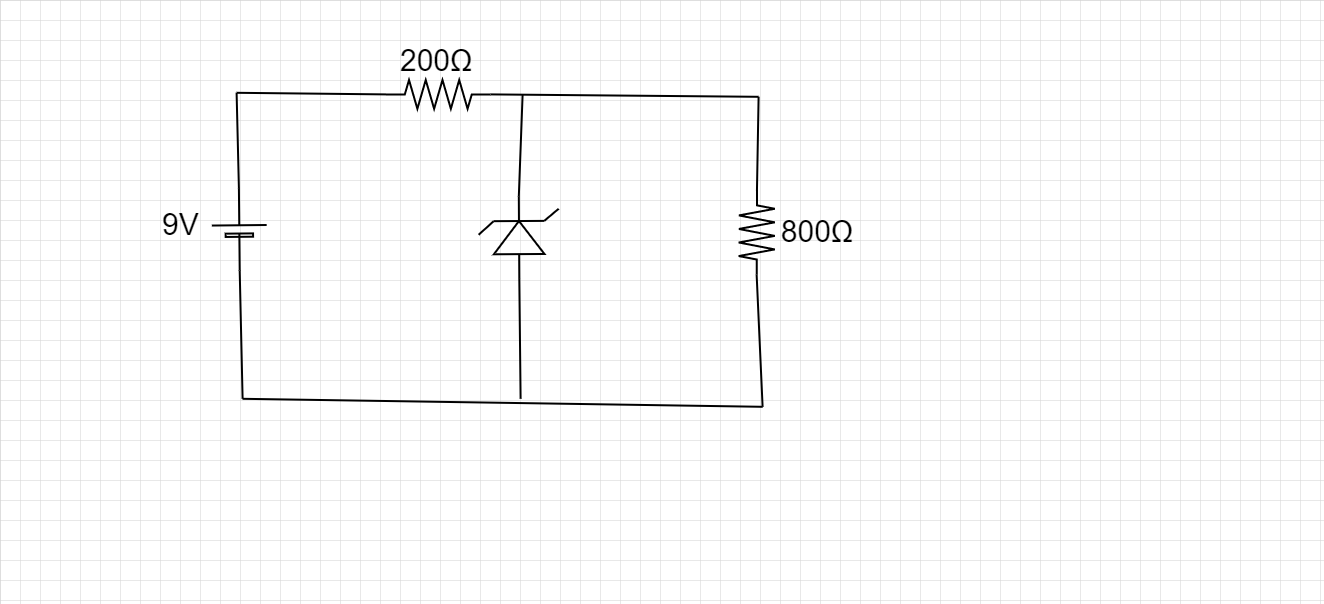
(A) $7mA$
(B) $17mA$
(C) $10mA$
(D) $15mA$

Answer 1

Hint
To solve this numerical, the first step is to apply Kirchhoff's junction law and create a current distribution over the circuit. Then the values of the different currents are calculated and then they are put back into the equation. Also because the load resistance of $800\Omega $ is in parallel with the Zener diode, the voltage around it is regulated. That is, the voltage across it is $5.6V$.

Complete step by step answer
Kirchhoff’s current (or junction) law states about conservation of charge in a circuit. So according to the law, the total current entering a junction is always equal to the total current entering a junction. Where junction refers to a common point of intersection for more than two wires. In our circuit, we can define B as a junction.
Let the current which leaves the battery be ${i_1}$. This ${i_1}$is the current which enters the junction B.
From here it divides into two smaller currents of ${i_2}$ and ${i_z}$. Where ${i_2}$ is the current which passes through the load resistance of $800\Omega $. While ${i_z}$is the current which passes through the Zener diode.
So the circuit diagram becomes-

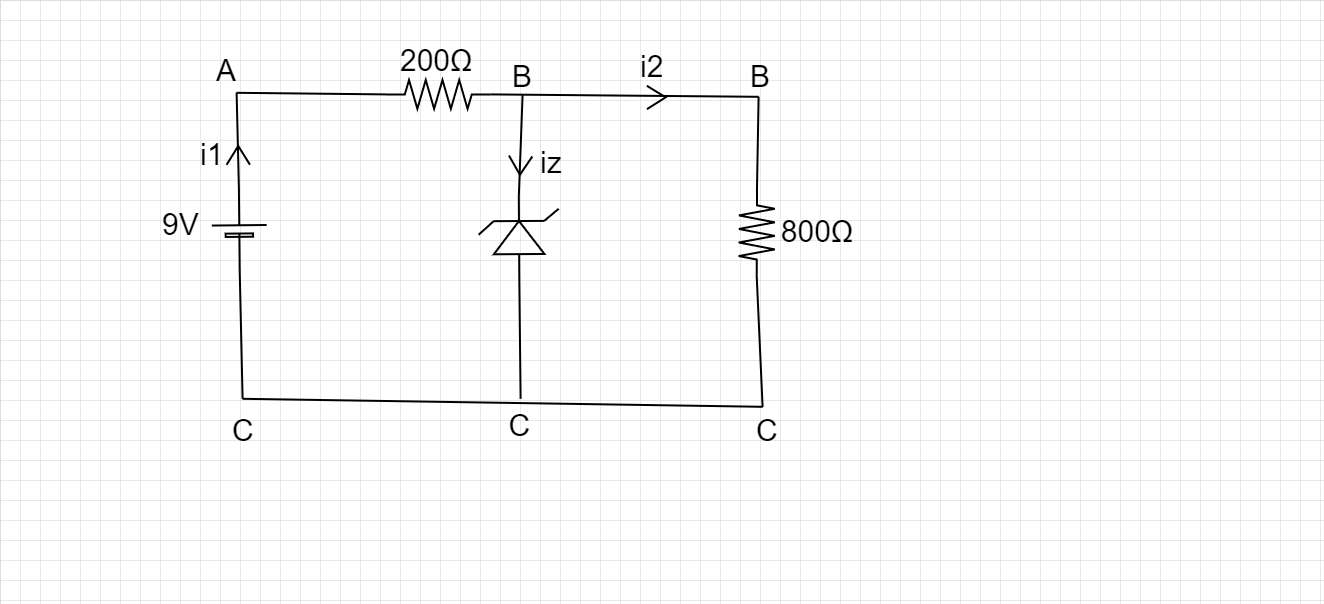
Applying Kirchhoff’s law, we have-
$\Rightarrow {i_1} = {i_2} + {i_z}$
Now, for ${i_2}$
We know that the Zener diode acts as a voltage regulator and thus voltage across the $\Rightarrow 800\Omega $ resistance is $5.6V$
$\Rightarrow i = \dfrac{V}{R}$ (Ohm’s law)
$\Rightarrow {i_2} = \dfrac{{5.6}}{{800}} = 7mA$
In a series connection voltage divides, therefore the voltage across $200\Omega $ resistances is equal to=
$\Rightarrow {V_{AB}} = 9 - {V_{BC}}$
$\Rightarrow {V_{AB}} = 9 - 5.6 = 3.4V$
Current across the $200\Omega $ is
$\Rightarrow {i_1} = \dfrac{{3.4}}{{200}} = 17mA$
Putting these values in Kirchhoff’s law,
We get,
$\Rightarrow {i_z} = {i_1} - {i_2}$
$\Rightarrow {i_z} = 17 - 10 = 10mA$
Thus the correct option is (C).

Note
While doing calculations which involve electrical circuits, you can write different points without any load (or other components) under the same name, because they all have the same potential. It has been done in the circuit diagram. This makes the calculations faster and more accurate.