Question

Determine the domain and range of \[{{\cos }^{-1}}x\].

Answer 1

Hint: We will be using the concept of inverse trigonometric functions to solve the problem. We will be using the fact that the functions that have inverse are one – one and onto. Also, we will use the graph of \[{{\cos }^{-1}}x\] to better understand the solution.

Complete step-by-step answer:
Now, we have to find the domain and range of \[{{\cos }^{-1}}x\].
We know that a function that has an inverse has exactly one output for exactly one input. To keep inverse trigonometric functions consistent with this definition. We have to designate ranges for them that will take care of all the possible input values and don’t have any duplication.
Now, we have the graph of \[\cos x\] as,

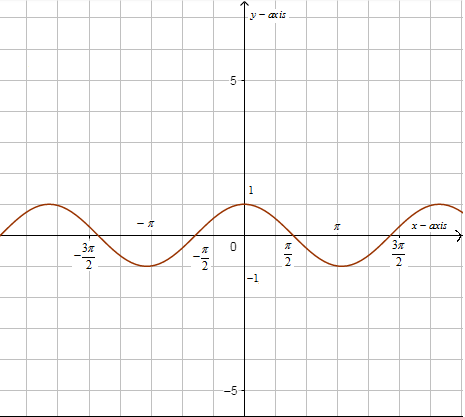
Now, we can see that the function \[\cos x\] is many to one that is for many values of x the output is the same.
Now, we know that the domain of an inverse trigonometric function is the same as that of the range of its counter trigonometric function.
Now, we know that the range of \[\cos x\] is $\left[ -1,1 \right]$. Therefore, the domain of \[{{\cos }^{-1}}x\] is $\left[ -1,1 \right]$ for this the range of function \[{{\cos }^{-1}}x\] on graph is,

So, we have the range of \[{{\cos }^{-1}}x\] as $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$.

Note: To solve these types of questions it is important to note that we have used a fact that the range of a function is equal to the domain of its inverse. Also the domain of function is equal to the range of its inverse. Also, the inverse of a function exists, if the function is one – one and onto.