
Determine the graph of the equation
Answer
405.3k+ views
Hint: To determine the graph we need different
Complete answer:
Given equation is
To plot a graph of the given equation
To find the first point let us put
On putting the value
On simplifying we get the value of
This means when
To find the second point we put
On putting the value
On taking 3 to another side
On simplifying we get the value of
On observing the values of
Now we make a table of these points.
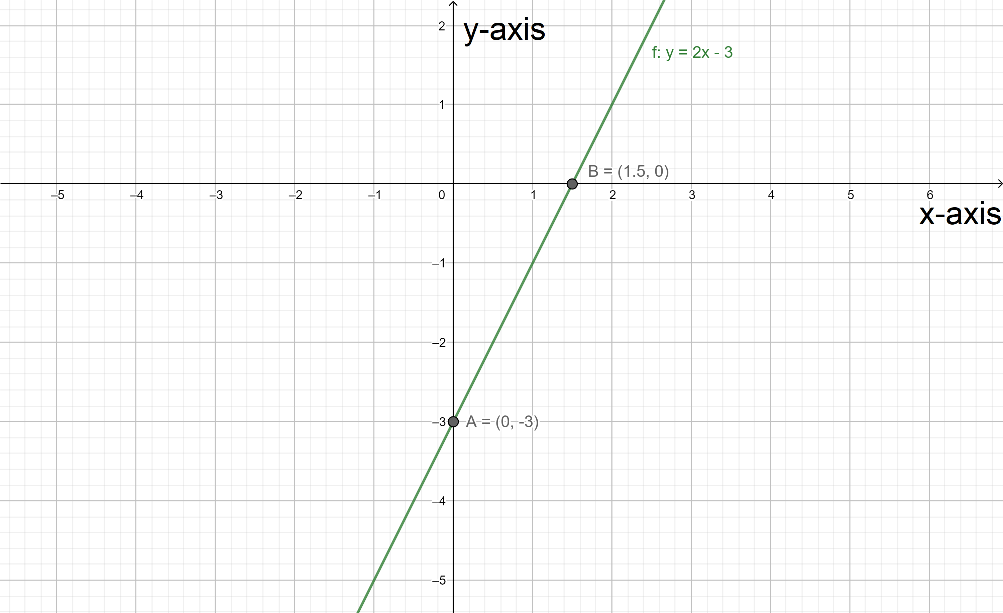
Now we put these points in the graph and join them to obtain the graph of the equation.
On putting these points in the graph. The graph looks like-
Note:
To plot the graph of the linear equation we need a minimum of two points but we are unable to make a line with a single point. More points are required if we make a curve then more points are required and with more points, our curve is more accurate.
Complete answer:
Given equation is
To plot a graph of the given equation
To find the first point let us put
On putting the value
On simplifying we get the value of
This means when
To find the second point we put
On putting the value
On taking 3 to another side
On simplifying we get the value of
On observing the values of
Now we make a table of these points.
| 0 | -3 |
| 1.5 | 0 |
Now we put these points in the graph and join them to obtain the graph of the equation.
On putting these points in the graph. The graph looks like-

Note:
To plot the graph of the linear equation we need a minimum of two points but we are unable to make a line with a single point. More points are required if we make a curve then more points are required and with more points, our curve is more accurate.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




