Question

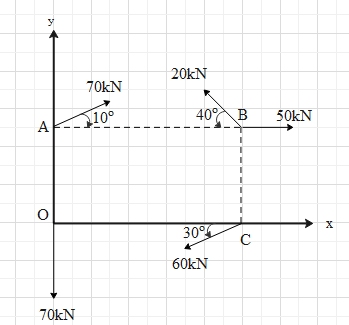
Determine the resultant moment about the origin of the given non-concurrent force system.

Answer 1

Hint: The magnitude of the torque about the origin is equal to the product of force and the perpendicular distance of the origin from the line of force. It is also equal to the product of the distance between the point at which the force is applied and the origin and the force perpendicular to the distance. If the force generates clockwise rotation then the torque is considered to be positive. If the torque generates an anticlockwise rotation then the torque is considered to be negative.
Formula used:
$\tau =F{{r}_{\bot }}={{F}_{\bot }}r$

Complete answer:
The torque or moment of force about origin due the a force acting at point is given as $\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$, where $\overrightarrow{F}$ is the force acting at that point and $\overrightarrow{r}$ is the position vector of the point at which the force is acting.
If we talk about the magnitude of torque, then its magnitude is given as $\tau =F{{r}_{\bot }}={{F}_{\bot }}r$, where ${{r}_{\bot }}$ is the perpendicular distance of the origin form the line of force and ${{F}_{\bot }}$ is the perpendicular force to the distance from the point and the origin.
If the force generates clockwise rotation then the torque is considered to be positive. If the torque generates an anticlockwise rotation then the torque is considered to be negative.
Let us first the torque by each force.
Consider the force of 70 kN.
The force perpendicular to ${{r}_{A}}$ is $70k\cos {{10}^{\circ }}=70k(0.98)=66.8kN$
And ${{r}_{A}}=2m$.
$\Rightarrow {{\tau }_{A}}=66.8k(2)=133.6kNm$
Consider the force of 60 kN.
The force perpendicular to ${{r}_{C}}$ is $60k\sin {{30}^{\circ }}=60k(0.5)=30kN$
And ${{r}_{C}}=4m$.
$\Rightarrow {{\tau }_{C}}=30k(4)=120kNm$
Let us find the torque due to the forces at point B.
Before that, resolve the force 20 kN into its horizontal and vertical components. Its horizontal component will be $20k\cos {{40}^{\circ }}=20k(0.76)=15.2kN$ and vertical component will be $20k\sin {{40}^{\circ }}=20k(0.64)=12.8kN$ as shown.

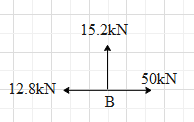
Now the net horizontal force at point B is $50k-15.2k=36.8kN$ in the direction of the positive x-axis.
And the vertical force is 12.8kN.
Therefore, the torque due to the horizontal force at the B is ${{\tau }_{B,1}}=(36.8k){{r}_{A}}=36.8k\times 2=73.6kNm$.
The torque due to the vertical force at B is ${{\tau }_{B,2}}=(12.8k){{r}_{C}}=12.8k\times 4=51.2kNm$.
However, the rotation due to ${{\tau }_{B,2}}$ will be in anticlockwise direction. Hence, ${{\tau }_{B,2}}=-51.2kNm$.
The torque due the force at point O is zero perpendicular distance is zero.
Therefore, the net torque about the origin is
$\tau ={{\tau }_{A}}+{{\tau }_{B}}+{{\tau }_{B,1}}+{{\tau }_{B,2}}=133.6k+120k+73.6k-51.2k=276kNm$.

Note:
The actual formula for the magnitude of the torque about the origin is given as $\tau =Fr\sin \theta $, F is the magnitude of the applied force, r is the distance of the origin from the point at which the force is applied and $\theta $ is the angle between F and r.