
How can I determine whether a horizontal parabola opens to the left or to the right?
Answer
454.2k+ views
Hint: A parabola can be horizontal, vertical, or tilted, depending upon the orientation of its axis. In the above question, we have been asked about a horizontal parabola, which means that its axis must be horizontal, that is, parallel to the x-axis. This means that the equation of the parabola must be linear in x and must be of the type
Complete step by step solution:
Since the parabola given in the above question is horizontal, its axis must be parallel to the x-axis. This implies that the equation of the parabola must be linear in x. So we can consider the general equation of a horizontal parabola as
Now, the direction of the opening of the parabola will depend on the sign of k in the above equation. On the basis of the signs of k, we can have two cases:
Case I: When k is positive
Considering again the equation of the horizontal parabola, we have
Since the LHS is equal to the square of y, it must be positive. This implies that the RHS, equal to the product
Now, we know that the region
This means that the parabola must open to the right for
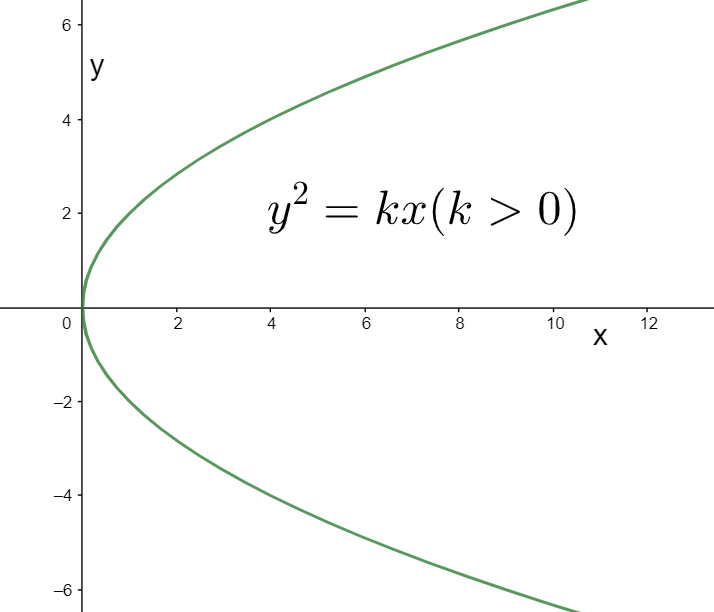
Case II: When k is negative
The parabolic equation is
In this case, the value of
We know that the region
This means that the parabola must open to the left for
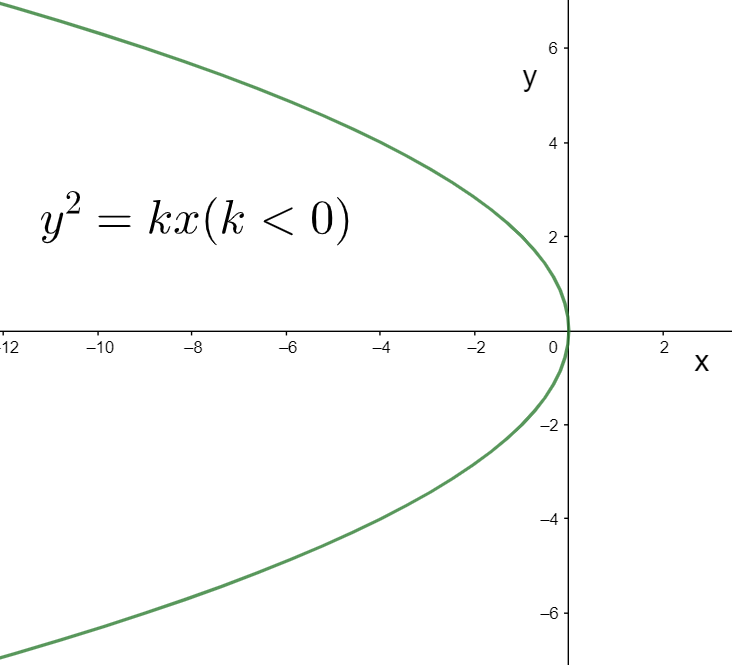
Hence, the parabola will open to the left when
Note: We must note that before deciding the direction of opening, it is necessary to write the equation of the parabola in the standard form of
Complete step by step solution:
Since the parabola given in the above question is horizontal, its axis must be parallel to the x-axis. This implies that the equation of the parabola must be linear in x. So we can consider the general equation of a horizontal parabola as
Now, the direction of the opening of the parabola will depend on the sign of k in the above equation. On the basis of the signs of k, we can have two cases:
Case I: When k is positive
Considering again the equation of the horizontal parabola, we have
Since the LHS is equal to the square of y, it must be positive. This implies that the RHS, equal to the product
Now, we know that the region
This means that the parabola must open to the right for

Case II: When k is negative
The parabolic equation is
In this case, the value of
We know that the region
This means that the parabola must open to the left for

Hence, the parabola will open to the left when
Note: We must note that before deciding the direction of opening, it is necessary to write the equation of the parabola in the standard form of
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




