Question

How do I determine whether a hyperbola opens horizontally or vertically?

Answer 1

Hint: First we know it is a horizontal or vertical hyperbola.
If it is a horizontal hyperbola since the $x$ term is positive.
\[\dfrac{{{{(x - h)}^2}}}{{{a^2}}} - \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1\]
That means the curves open left and right.
If it is a vertical hyperbola since the $y$ term is positive.
 $\dfrac{{{{(y - k)}^2}}}{{{a^2}}} - \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1$
That means the curves open up and down.

Complete step by step answer:The graph of a hyperbola creates two smooth curves as pictured here:

There are two patterns for hyperbolas:
Horizontal:
\[\dfrac{{{{(x - h)}^2}}}{{{a^2}}} - \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1\]
Vertical:
$\dfrac{{{{(y - k)}^2}}}{{{a^2}}} - \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1$
We can determine the following:
If it is vertical or horizontal:
If the $x$ term is positive, the parabola is horizontal (the curves open left and right). The equation is,
\[\dfrac{{{{(x - h)}^2}}}{{{a^2}}} - \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1\]
The horizontal parabola graph is

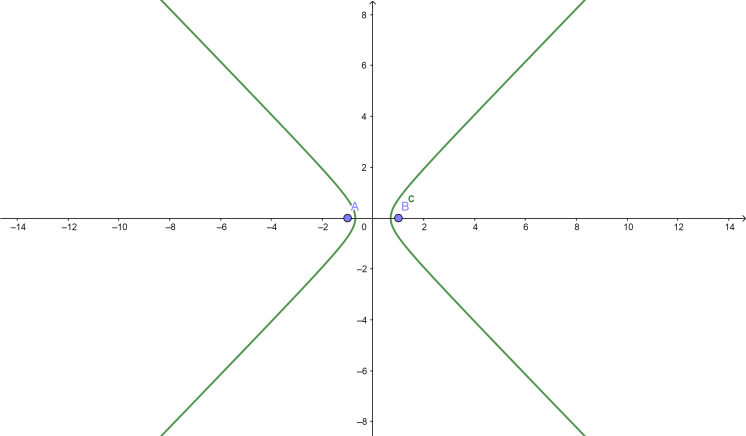
If the $y$ term is positive, the parabola is vertical (the curves open up and down). The equation is
$\dfrac{{{{(y - k)}^2}}}{{{a^2}}} - \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1$
The vertical parabola graph is

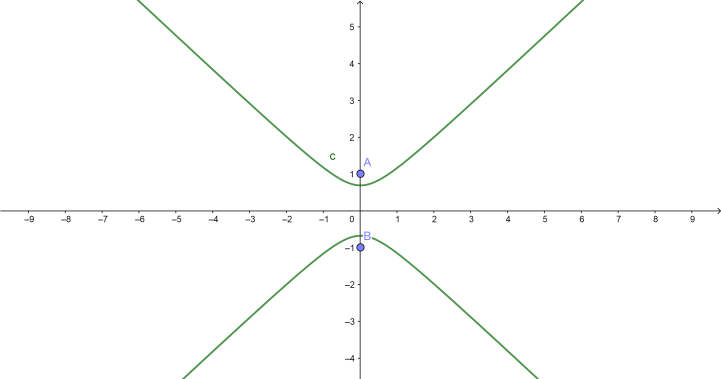
The center point as with all conic sections, the center points $(h,k)$ . Notice that the $h$ is always with the $x$ and the $k$ is always with the $y$ . There is also a negative in front of each, so you must take the opposite.
The $a$ and $b$ values will be needed to graph the parabola. Notice that $a$ is always under the positive term and $b$ is always under the negative.

Note:
Notice that $(h,k)$ is the center of the entire hyperbola but does not fall on the hyperbola itself. Each hyperbola has a vertex and two asymptotes guide how wide or how narrow the curve.
If $x$ is on the front, the hyperbola opens horizontally.
If $y$ is on the front, the hyperbola opens vertically.