
How many diagonals does a regular pentagon have?
(a) 3
(b) 4
(c) 5
(d) 6
Answer
520.5k+ views
Hint: For solving this question first we will see the that diagonal is the line segment that joins two no-adjacent vertices so, we will derive the formula
Complete step by step answer:
Given:
We have to find the number of diagonals for a regular pentagon.
Now, before we proceed we should know how to select
Now, we should know that in a polygon, the diagonal is the line segment that joins two non-adjacent vertices. Moreover, as we know that in case of any
Now, from the above discussion, we conclude that for any
Now, we come back to our question in which we have to find the number of diagonals for a regular pentagon. As we know that in a regular pentagon there are a total of 5 sides which means the value of
Number of diagonals for the regular pentagon
For more clarity look at the figure given below:
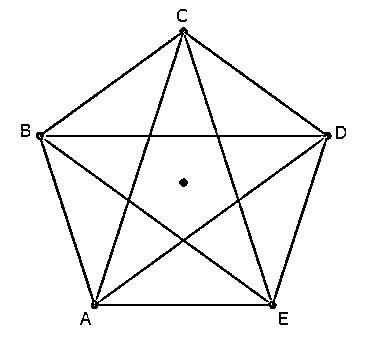
In the above figure, we have a regular pentagon ABCDE with its five diagonals AD, AC, BD, BE and CE.
Thus, a regular pentagon has 5 diagonals.
Hence, (c) is the correct option.
Note: Here, the student before solving first try to understand the problem and we should apply the formula of the selection of
Complete step by step answer:
Given:
We have to find the number of diagonals for a regular pentagon.
Now, before we proceed we should know how to select
Now, we should know that in a polygon, the diagonal is the line segment that joins two non-adjacent vertices. Moreover, as we know that in case of any
Now, from the above discussion, we conclude that for any
Now, we come back to our question in which we have to find the number of diagonals for a regular pentagon. As we know that in a regular pentagon there are a total of 5 sides which means the value of
Number of diagonals for the regular pentagon
For more clarity look at the figure given below:

In the above figure, we have a regular pentagon ABCDE with its five diagonals AD, AC, BD, BE and CE.
Thus, a regular pentagon has 5 diagonals.
Hence, (c) is the correct option.
Note: Here, the student before solving first try to understand the problem and we should apply the formula of the selection of
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What is the past participle of wear Is it worn or class 10 english CBSE

What is the full form of POSCO class 10 social science CBSE

How fast is 60 miles per hour in kilometres per ho class 10 maths CBSE

Choose the feminine form of the given noun Fox AFoxess class 10 english CBSE




