Question

How many diagonals does a regular pentagon have?
\[
  A.{\text{ 3}} \\
  B.{\text{ 4}} \\
  C.{\text{ 5}} \\
  D.{\text{ 6}} \\
 \]

Answer 1

Hint: Use the relation between the number of sides of any figure and the number of diagonals of the figure to find out directly the number of diagonals. Using diagrams for finding can also be done.

Complete step-by-step answer:
Given shape is a regular pentagon. We know that a regular pentagon has 5 sides.

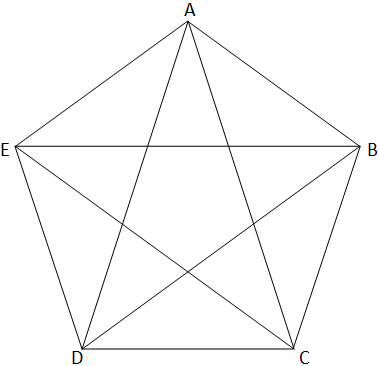
Also we know the relation between the number of sides and number of diagonals of the figure.
If a figure has “n” number of sides in it then the number of diagonals of the figure is given by
$ \Rightarrow {\text{ Number of diagonals}} = \dfrac{{n\left( {n - 3} \right)}}{2}$
For regular pentagon number of sides = 5.
$ \Rightarrow n = 5$
So the number of diagonals of regular pentagon is given as:
$
   \Rightarrow {\text{ Number of diagonals}} = \dfrac{{n\left( {n - 3} \right)}}{2} \\
   \Rightarrow {\text{ Number of diagonals}} = \dfrac{{5\left( {5 - 3} \right)}}{2} \\
   = \dfrac{{5 \times 2}}{2} = 5 \\
 $
Hence, the number of diagonals of a regular pentagon is 5, which is also visible from the above figure.
So, option C is the correct option.

Note: Such type of question can also be done by simply drawing the figure and visualizing the result from the figure. But this method cannot be used when the number of sides in the figure will be very large. So remembering formulas is very important for solving such problems. Also students must remember that this formula has been derived by the method of permutation and combination.