Question

How many diagonals does the following have: convex quadrilateral.

Answer 1

Hint: We know that convex quadrilateral is a four-sided polygon and each interior angle is less than $180{}^\circ $. We will find the number of diagonals in the convex quadrilateral by analyzing through it’s figure.

Complete step-by-step answer:
Diagonal is a line segment which joins two vertices of a polygon, in which these vertices do not lie on the same edge and we know that by definition of convex quadrilateral, all diagonals of convex quadrilateral always lie inside it.
Convex quadrilateral is a four-sided polygon that means it has four vertices, two vertices which do not lie on the same edge from a diagonal.
We will draw a convex quadrilateral and let four vertices be A, B, C, D.

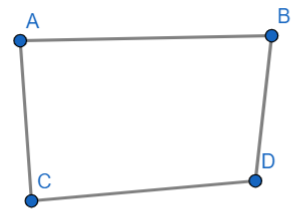
First, we will try to join two vertices such that it should be a diagonal.
So, the diagonal will be possible by joining the vertices A and D.

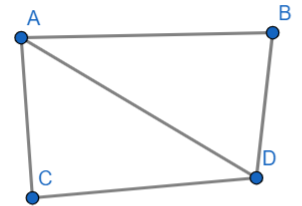
Then another diagonal is possible by joining the vertices B and C.

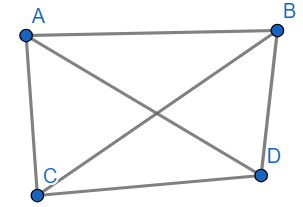
Then we will check the possibility of another diagonal. We cannot draw another diagonal. So, the total count of diagonals we drew was 2.
We observed from above figures that there will be two diagonals in convex quadrilateral.
Hence, “The number of diagonals that a convex quadrilateral has is 2.”

Note: In this type of questions, analyzing the geometric figures or by finding through mathematical induction is the best way to solve a question. All the diagonals of the convex quadrilateral lie inside the quadrilateral.