Question

How many diagonals does the regular hexagon have?
(a) 8
(b) 9
(c) 10
(d) 11

Answer 1

Hint: We solve this problem by taking the regular hexagon and the list of diagonals.
We have the condition the regular hexagon has 6 sides of equal length. By using this statement we take the regular hexagon of 6 sides and then we take all the possible diagonals and count them to get the number of diagonals.

Complete step by step answer:
We are asked to find the number of diagonals of the regular hexagon.
Let us assume a regular hexagon ABCDEF as follows

Now, let us join all the possible vertices in the above hexagon then we get

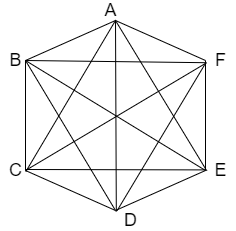
Now, let us take the list of all possible diagonals in the above figure then we get
(1) AC
(2) AD
(3) AE
(4) BD
(5) BE
(6) BF
(7) CE
(8) CF
(9) DF
Here, we can see that we have a total of 9 diagonals
Therefore we can conclude that the number of diagonals of a regular hexagon is 9
So, option (b) is the correct answer.

Note:
 We can solve this problem in another method also.
We are asked to find the number of diagonals for regular hexagons.
We know that a regular hexagon has 6 sides.
We have the direct formula for number of diagonals of \[n\] sided regular polygon as
\[N=\dfrac{n\left( n-3 \right)}{2}\]
By using the above formula to regular hexagon which has 6 sides then we get
\[\begin{align}
  & \Rightarrow N=\dfrac{6\left( 6-3 \right)}{2} \\
 & \Rightarrow N=3\times 3=9 \\
\end{align}\]
Therefore we can conclude that the number of diagonals of regular hexagon is 9
So, option (b) is the correct answer.