Question

Diagonals of a rhombus are 12cm and 16cm respectively, then find the side of the rhombus and its perimeter.

Answer 1

Hint: Rhombus is a two dimensional shape with four equal sides and four angles which can or cannot be $90{}^\circ $, but opposite angles are always same, and both diagonals of a rhombus are perpendicular and bisect each other.

Complete step by step answer:
According to given data,

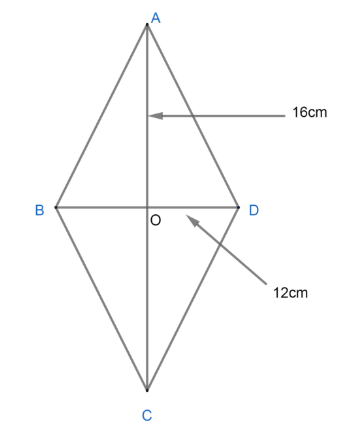
Shape ABCD is a rhombus and O is the intersecting point of both diagonals which is bisecting both diagonals, and both diagonals are perpendicular to each other according to definition.
$\begin{align}
  & \Rightarrow AO=\dfrac{16}{2}cm=8cm \\
 & \Rightarrow BO=\dfrac{12}{2}cm=6cm \\
\end{align}$
So, $\Delta AOB$ is a right triangle, and using Pythagoras Theorem we can find the length of AB which is a side of rhombus.
According to Pythagoras Theorem,
\[\begin{align}
  & A{{B}^{2}}=B{{O}^{2}}+A{{O}^{2}} \\
 & AB=\sqrt{{{6}^{2}}+{{8}^{2}}}cm \\
 & AB=\sqrt{36+64}=\sqrt{100}=10cm \\
\end{align}\]
And we know the perimeter of the rhombus is equal to 4a where ‘a’ is the length of a side.
So, Perimeter of rhombus $=4a$
$\begin{align}
  & =4\times 10cm \\
 & =40cm \\
\end{align}$
Hence, the side is 10cm and the perimeter is 40cm.

Note: Here we should have appropriate knowledge of general shapes, some time lack of knowledge can confuse us in easy problems. By the way here we can use direct formula to find out the length of side which is $4A{{B}^{2}}=A{{C}^{2}}+B{{D}^{2}}$.