Question

What is the difference between the complementary and supplementary angles of $ {{70}^{\circ }} $ ?
(a) $ {{60}^{\circ }} $
(b) $ {{70}^{\circ }} $
(c) $ {{80}^{\circ }} $
(d) $ {{90}^{\circ }} $

Answer 1

Hint: We will use definitions of complementary and supplementary angles to find the complementary and supplementary angles of 70° and take their difference to get the answer. But before that we should know the both of the definitions, (1) Two angles are called complementary angles, if their sum is equal to one right angle i.e. 90°. And, (2) Two angles are called supplementary angles, if their sum is equal to two right angles i.e. 180°.

Complete step-by-step answer:
Two angles are called complementary angles, if their sum is equal to one right angle i.e. 90°. Each angle is called the complement of the other. Example, 20° and 70° are complementary angles, because 30° + 60° = 90°. And,
Two angles are called supplementary angles, if their sum is equal to two right angles i.e. 180°.Each angle is called the supplement of the other. Example, 30° and 150° are supplementary angles, because 30° + 150° = 180°.
Let us suppose the complementary angle of 70° be X°, so
70°+ X° = 90°
Taking 70° to the R.H.S., we get
X° = 90° - 70°
X° = 20
we can see the figure of complementary angles,

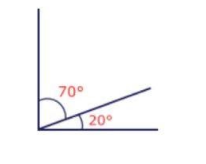
Hence complementary angle of 70° is 20°
Now for supplementary angle of 70°,
Let us suppose the supplementary angle of 70° be Y°, so
70°+ Y° = 180°
Taking 70° to the R.H.S., we get
Y° = 180° - 70°
Y° = 110°
we can see the figure of supplementary angles,

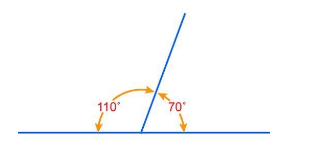
Difference between supplement and complement = Y° - X°
=110°-20°
=90°
So, the correct answer is “Option D”.

Note: Above question can also be solved for any general value of angle instead of 70°. Suppose any random angle A° it’s supplementary angle is given by (180°-A°) and it’s complementary angle is given by (90°-A°) now, difference of supplementary and complementary angles is given by,
(180°- A°) - (90°- A°) = 180° - A° - 90° + A° = 90°
Hence the difference of supplementary and complementary angle is always 90°.