Question

What is the difference between the cross product and dot product of two vectors? Or if a force of $10$ Newton’s at an angle of $30^\circ $ above horizontal is used to drag a block $6$ meters, how much work is done?

Answer 1

Hint: First we will define what is the definition of cross product and dot product of two vectors. Then comparing both of them we can find the differences. Now for the second part we will first draw a rough diagram showing all the parameters required to solve this problem. Then using a work done formula when force and displacement vectors are known to us.

Complete step by step answer:
Cross product: Cross product is also known as a vector product of two vectors. Let $\overrightarrow A $ and $\overrightarrow B $ are the two vectors and cross product of these two are denoted as $\overrightarrow A \times \overrightarrow B $ and its resultant vectors is perpendicular to the two vectors $\overrightarrow A $ and $\overrightarrow B $.
$\overrightarrow A \times \overrightarrow B = |\overrightarrow A ||\overrightarrow B |\sin \theta $

Dot product: Dot product is also known as the scalar product of two vectors. Let $\overrightarrow A $ and $\overrightarrow B $ are the two vectors and dot products of these two are denoted as $\overrightarrow A \cdot \overrightarrow B $.
$\overrightarrow A \cdot \overrightarrow B = |\overrightarrow A | \cdot |\overrightarrow B |\cos \theta $
Hence on comparing these two definitions the major difference between cross product and dot product is that cross product is product of magnitude of vectors and the sine of the angle in which they subtend each other while dot product is the product of magnitude of the vectors and the cos between them.

As per the problem , a force of $10$ Newton’s at an angle of $30^\circ $ above horizontal is used to drag a block $6$ meters. Now we need to calculate the work done by the block.

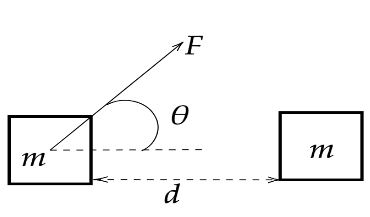
We know, $F = 10N$, $\theta = 30^\circ $ and $d = 6\,m$. Now we know that work din in moving a body through a distance d by a force F at an angle $\theta $ is denoted by,
$W = F \cdot d$
$ \Rightarrow W = |F||d|\cos \theta $
Now putting the given values we will get,
$W = \left( {10N} \right)\left( {6m} \right)\cos 30^\circ \\
\Rightarrow W= 60\dfrac{{\sqrt 3 }}{2} \\
\therefore W= 30\sqrt 3\, J$

Hence,the work done is $30\sqrt 3\, J$.

Note: Remember that the dot product is a scalar while a cross product is vector. As work done is the product of two dot vectors then it is a scale quantity. Scalar quantities are those which don't depend on direction of the motion; it only depends on the magnitude while vector quantities depend on both.